Dirichlet boundary conditions

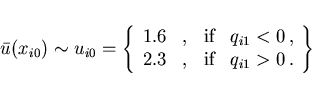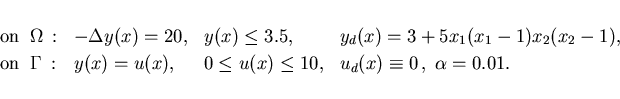
Example 5.1: To enable a comparison, we consider first the example in Bergounioux, Kunisch [3], Section 5.2, with the following data:

$$\begin{eqnarray*} \hspace*{-10mm} \begin{array}{llll} \mbox{on} \;\;\Omega \,: &... ...) \leq 10 , & u_d(x) \equiv 0 \,, \; \alpha = 0.01 . \end{array}\end{eqnarray*}$$

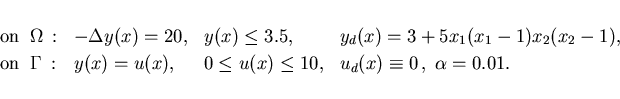
The following results were obtained, they are explained below:

Cost functional : $F(\bar{y},\bar{u}) = 0.196525$, CPU seconds : 96

Figure 1: Optimal control for Example 5.1

The optimal control is shown in Figure 1. The optimal state and adjoint variable are not shown here, because they are very similar to those in Figure 3 where $\,\alpha=0.01\,$ is replaced by $\,\alpha=0.0\,$. It should be noted that the output of Lagrange multipliers is provided by AMPL. It is no difficulty for primal-dual methods to produce multipliers since, in fact they are variables that are computed simultaneously with the primal problem variables. The control constraints are not active while the state variable attains its upper bound only in the center $\,x_{ij}:=(0.5,0.5)\,$ of the unit square with dual variable $\, \mu_{ij} = .24602\,$. This is in agreement with the results in [3]. It can be checked that the adjoint equation (3.6) holds in the discretized version with $\, \Delta_h \,$ denoting the discretized Laplacian,

$$\begin{eqnarray*} \begin{array}{ll} -\Delta_h \,\bar{q}(x) + \bar{y}(x) - y_d(x... ...mu_{ij}/h^2 = 0 & \; \mbox{for} \quad x = x_{ij} \,. \end{array}\end{eqnarray*}$$

We verify the second equation in the active gridpoint $\,x_{ij}=(0.5,0.5)\,$ where the following data were obtained: $\; q_{ij}=-0.21312,\; q_{i-1,j}=-0.15161,\; y_{ij}=3.5, \;y_{ij} - y_d(x_{ij}) = 0.1875,\; \mu_{ij}/h^2 = 2460.2\,.$ Note that the adjoint function is symmetric around $\,x_{ij}\,$. Hence the adjoint equations hold with $\, -\Delta_h\,\bar{q}(x_{ij}) = 4*(q_{ij}-q_{i-1,j})/h^2 = - 2460.40 \,$ and $\,y_{ij} - y_d(x_{ij}) + \mu_{ij}/h^2 = 2460.39\,$. The measure $\,\bar{\mu}\,$ in (3.6) is a delta distribution, $\,\bar{\mu} = \bar{\nu}_s\cdot \delta(x-x_{ij})\,,$ with $\,\bar{\nu}_s \sim \mu_{ij}= 0.24602 \,$ in view of (4.12).

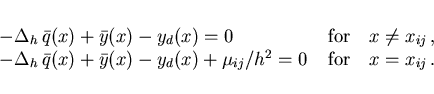
This example will also be used to illustrate the numerical process in more detail.

Table 1: Detailed information on solution of Example 5.1

N+1	it	AMPL	LOQO	Acc	$F(\bar{y},\bar{u})$	$y(.4,.5)$	$u(0,.5)$
50	25	1	10	8	.188170	3.449184	1.686801
100	26	6	96	8	.196525	3.449163	1.690270
200	29	23	1477	8	.200772	3.449158	1.692029

In Table 1 we summarize the data: size of grid, number of iterations of LOQO, times in seconds for the AMPL compilation and the solution by LOQO, the accuracy as the number of correct significant digits in the objective function value. The primal-dual approach yields upper and lower bounds for this value and thus permits such a statement. In all the following examples this accuracy measure was at least 8 and is therefore not listed. Finally, we list the objective function value and one representative value of both the state and the control variable. While the state variable not far from the active center point has a small error, the control at the midpoints of the edges still varies in the fourth digit. Thus, $N+1=100$ was chosen for the subsequent calculations. Since the AMPL times were in the range of a few seconds or a few percent of the solution times they will not be given below.

Table 2: Comparison of different solvers on Example 5.1

N+1	LANCELOT	LOQO	MINOS	SNOPT	BPMPD
50	7.1	1	5.6	8	.5
70	15.4	1	10.2	(unbd)	.3
90	16.2	1	(inf)	(unbd)	.28
200	-	1	-	-	.14

We compare LOQO and other solvers with AMPL interface available to us in Table 2. For $N+1=100$ not all the codes considered (LANCELOT-A, MINOS-5.5, SNOPT-5.3, BPMPD-2.21; links to all codes in [21]) were successful. Therefore, results are listed for several coarser grids as well as for the finest grid used with LOQO. Given are CPU times on the same platform used above, but scaled to LOQO's time. MINOS reports one problem as infeasible while SNOPT reports two problems as unbounded. The reason for these messages may also be a "bad starting guess". All solvers were given the same AMPL file and AMPL initializes variables with zero. For $N+1=200$ all solvers except LOQO and BPMPD exceeded the available memory (256MB). The convex QP code BPMPD solves with increasing efficiency compared to LOQO but this is only possible, because, in fact, Example 5.1 is a convex QP problem. BPMPD is not applicable to most of the other examples solved below. For another comparison see Example 5.7.

Example 5.2: All data are the same as in Example 5.1 except that we choose $\,\alpha=0.0\,$ instead of $\,\alpha=0.01\,$. According to the optimal control law (3.11) we can expect either a bang-bang or a singular control. We find the following results:

Cost functional : $F(\bar{y},\bar{u}) = .096695$, CPU seconds : 78

The optimal control, adjoint variable and optimal state are shown in Figures 2 and 3. Both the control and state constraints do not become active. Hence, the optimal control is totally singular on $\,\Gamma\,$. This is in accordance with the control law (3.11) since the normal derivative of the adjoint variable satisfies $\, \partial_{\nu}\bar{q}\vert _{\Gamma} \equiv 0 \,$ which follows from the numerical results $\,q_{i1} \equiv 0 \,$ in view of (4.4). In Figure 3 as in Figures 5 and 7 below the vertical axis is labeled $y/u$ since for these examples both the state and the control are plotted in these figures.

Figure 2: Optimal control and adjoint variable for Example 5.2

Figure 3: Optimal state for Example 5.2

Example 5.3: The data are the same as in Example 5.1 except that we choose more restrictive state and control constraints:

$$\begin{eqnarray*} \hspace*{-11mm} \begin{array}{llll} \mbox{on} \;\;\Omega \,: &... ...\leq 2.3 , & u_d(x) \equiv 0 \,, \; \alpha = 0.01 . \end{array}\end{eqnarray*}$$

Figure 4: Optimal control and switching function for Example 5.3

Figure 5: Optimal state and adjoint variable for Example 5.3

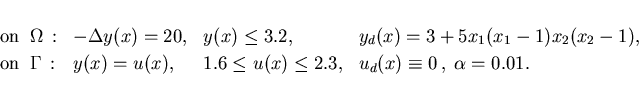
We obtain the following results:

Cost functional : $F(\bar{y},\bar{u}) = .321010$, CPU seconds : 103

The optimal control, state and adjoint variable are shown in Figures 4 and 5. The optimal control is continuous and has two boundary arcs with $\,\bar{u}(x) = 2.3 \,$ and one boundary arc with $\,\bar{u}(x) = 1.6 \,$. The junction points with the boundary are the points $\,x_1=(.02,0), \,x_2=(.18,0) , \,x_3=(.23,0), \,x_4=(.77,0), \,x_5=(.82,0) , \,x_6=(.98,0)\,$ on the bottom edge of $\,\Gamma\,$. By inspecting the switching function in Figure 4, we can verify the control law (3.10). The assumption $\,b_u \equiv 1 \,$ underlying (3.10) obviously holds. Let us check the control condition on the bottom edge of $\,\Gamma\,$ at the points $\,x_{i0}\,$. Observe that $\,\partial_{\nu}\bar{q}(x_{i0}) \sim -q_{i1}/h\,$ according to (4.22) since we have $\,q_{i0}=0\,$. Then in view of $\,\alpha = h = .01 \,$ the control law (3.10) takes the form

$$\begin{eqnarray*} \bar{u}(x_{i0}) \,\sim \, u_{i0} = \left \{ \begin{array}{llll... ...\mbox{if} & q_{i1} * 10^4 \, \geq 2.3 \,. \end{array}\right \} \end{eqnarray*}$$

The active set for the state constraint $\, y(x) \leq 3.2 \,$ is the center point $\,\bar{x}=x_{ij}=(0.5,0.5)\,$. The dual variable for this active inequality constraint is $\, \mu_{ij} = .642712\,$. Again, with these data the validity of the adjoint equation (3.6) can be verified in its discretized form.

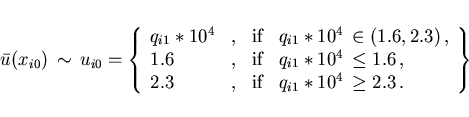
Example 5.4: The data are those from Example 5.3 but now we choose $\,\alpha=0.0\,$ expecting to obtain a bang-bang control in contrast to the totally singular control in Example 5.2. This expectation is met with the following results:

Cost functional : $F(\bar{y},\bar{u}) = .249178$, CPU seconds : 116

The optimal control shown in Figure 6 is indeed bang-bang. The switching function on the bottom edge of $\,\Gamma\,$ is $\,\partial_{\nu}\bar{q}(x_{i0}) \sim -q_{i1}/h\,$ according to (4.22). Then Figure 6 clearly illustrates the control law (3.11):

$$\begin{eqnarray*} \bar{u}(x_{i0}) \sim u_{i0} = \left \{ \begin{array}{llllll} 1... ...\\ 2.3 & , & \mbox{if} & q_{i1} > 0 \,. \end{array}\right \} \end{eqnarray*}$$

The switching points on the bottom edge are $\, x_1 = (.2,0), \, x_2= (.8,0) \,$. Again, the optimal state displayed in Figure 7 is active at the center point $\,\bar{x}=x_{ij}=(0.5,0.5)\,$. The dual variable for this active inequality constraint is $\, \mu_{ij} = .733781\,$.

Figure 6: Optimal control and switching function for Example 5.4

Figure 7: Optimal state and adjoint variable for Example 5.4