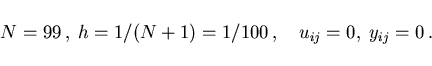We consider elliptic problems with the following specifications:
the cost functional is of tracking type (2.13), the elliptic operator
in (2.2) is the Laplacian
![]() on the unit square
on the unit square
![]() and the control and state
constraints are box constraints given in (2.14).
The choice of symmetric functions
and the control and state
constraints are box constraints given in (2.14).
The choice of symmetric functions ![]() and
and
![]() in the tracking functional, implies that the optimal
control is the same on every edge of
in the tracking functional, implies that the optimal
control is the same on every edge of
![]() However, we have treated the discretized controls on every edge of
However, we have treated the discretized controls on every edge of ![]() as independent optimization variables. The symmetry of the optimal control
will then be a result of the optimization procedure.
as independent optimization variables. The symmetry of the optimal control
will then be a result of the optimization procedure.
Tests for the following examples were run with different stepsizes
and starting values. For convenience, in the sequel we shall report
on results obtained for fixed stepsize and starting values: