The following elliptic control problem with control and state constraints
generalizes the elliptic problems considered in
Bergounioux, Kunisch [3], Ito, Kunisch [16].
When admitting Dirichlet boundary conditions,
the functions ![]() in the cost functional (2.1),
in the cost functional (2.1),
![]() in the boundary conditions (2.2),
and
in the boundary conditions (2.2),
and ![]() in the constraints (2.3) do not depend on the
state variable
in the constraints (2.3) do not depend on the
state variable ![]() . This leads to the problem of
finding a control
. This leads to the problem of
finding a control
![]() that minimizes the functional
that minimizes the functional
When treating Dirichlet boundary conditions, an intrinsic difficulty
arises from the fact that the solution operator
![]() for (3.2) is not sufficiently smooth
as to give an appropriate form of first order necessary conditions:
cf., Lions [19], Lions, Magenes [20], Chapter 2.
A weak formulation of first
order necessary conditions for linear elliptic equations
may be found in Bergounioux, Kunisch [3].
Instead of trying to prove first order necessary conditions
under strong assumptions
we content ourselves with deriving first order
necessary conditions in a purely formal way.
This form of the necessary conditions will be
justified by its analogy in
the first order necessary conditions for the discretized version
of the elliptic problem; cf. Section 4.2.
for (3.2) is not sufficiently smooth
as to give an appropriate form of first order necessary conditions:
cf., Lions [19], Lions, Magenes [20], Chapter 2.
A weak formulation of first
order necessary conditions for linear elliptic equations
may be found in Bergounioux, Kunisch [3].
Instead of trying to prove first order necessary conditions
under strong assumptions
we content ourselves with deriving first order
necessary conditions in a purely formal way.
This form of the necessary conditions will be
justified by its analogy in
the first order necessary conditions for the discretized version
of the elliptic problem; cf. Section 4.2.
Denote an optimal solution of problem (3.1)-(3.4)
by ![]() and
and ![]() . The active sets
of inequality constraints (3.3) and (3.4) are
. The active sets
of inequality constraints (3.3) and (3.4) are
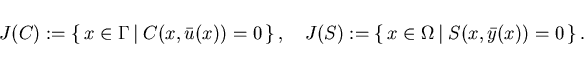
Let ![]() and
and ![]() be multipliers associated with the elliptic
equation and the Dirichlet boundary
condition in (3.2), and let
be multipliers associated with the elliptic
equation and the Dirichlet boundary
condition in (3.2), and let ![]() resp.
resp. ![]() be the
multiplier resp. the Borel measure associated with the control and state inequality constraints
(3.3) and (3.4). Then the Lagrangian for
problem (3.1)-(3.4) becomes
be the
multiplier resp. the Borel measure associated with the control and state inequality constraints
(3.3) and (3.4). Then the Lagrangian for
problem (3.1)-(3.4) becomes
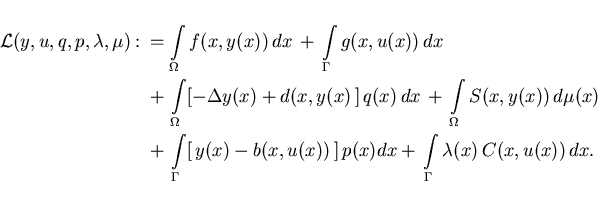
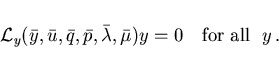
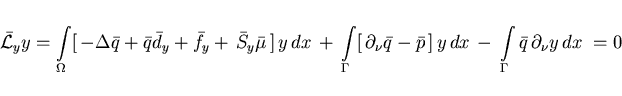
![\begin{displaymath}
\bar{\cal L}_u\,u =
[\,\bar{g}_u + (\partial_{\nu}\bar{q})\...
...{\lambda} \bar{C}_u\,]u \, = 0
\quad \mbox{for all} \;\; u \,,
\end{displaymath}](img95.gif)
Note that the minimum condition (3.8) agrees with the condition
(2.9) if we replace ![]() formally by
formally by
![]() .
Hence, assuming functionals of tracking type (2.12),
box constraints (2.13) for control and state
and the property
.
Hence, assuming functionals of tracking type (2.12),
box constraints (2.13) for control and state
and the property
![]() , we obtain the counterparts of
the control laws (2.16), (2.17).
, we obtain the counterparts of
the control laws (2.16), (2.17).
Case
![]() : the control is determined by
: the control is determined by
Case ![]() : the optimal control is of bang-bang
or singular type
: the optimal control is of bang-bang
or singular type