

Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Neumann boundary conditions
The Dirichlet boundary conditions in (3.2) are
incorporated by the relations
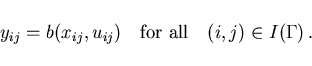 |
(4.15) |
Hence it suffices to work with a reduced number
of optimization variables in (4.1), namely we can take
The equality constraints
agree with those from (4.3),
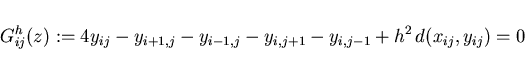 |
(4.16) |
for all indices
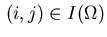 where
the values
where
the values 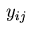 on the boundary are substituted from
the relations (4.15).
The control and state inequality constraints (3.3) resp.
(3.4) give rise to the inequality constraints:
on the boundary are substituted from
the relations (4.15).
The control and state inequality constraints (3.3) resp.
(3.4) give rise to the inequality constraints:
| |
|
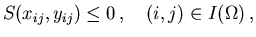 |
(4.17) |
| |
|
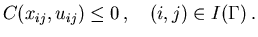 |
(4.18) |
Finally, the cost function is derived from (3.1) as
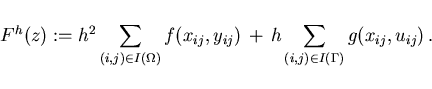 |
(4.19) |
By means of (4.16)-(4.19) we have obtained
an NLP-problem of the form (4.1).
Let us evaluate the first order optimality conditions of Kuhn-Tucker type
for problem (4.16)-(4.19).
The Lagrangian function becomes
where the Lagrange multipliers
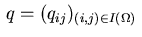 ,
,
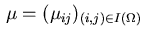 and
and
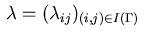 which
are associated with the equality constraints (4.16),
the inequality constraints (4.17),
and the inequality constraints (4.18).
The multipliers
which
are associated with the equality constraints (4.16),
the inequality constraints (4.17),
and the inequality constraints (4.18).
The multipliers 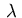 and
and 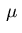 satisfy the complementarity
conditions corresponding to (3.9):
satisfy the complementarity
conditions corresponding to (3.9):
In the next step we discuss the necessary conditions of optimality
for different combinations of indices 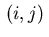 .
For indices
.
For indices
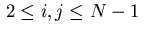 we obtain the relations
we obtain the relations
Hence, for this set of indices we see that the Lagrange multipliers
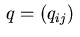 satisfy the five-point-star difference equations for the adjoint equation
satisfy the five-point-star difference equations for the adjoint equation
 in
(3.6)
if we use the same identification for the Borel measure
in
(3.6)
if we use the same identification for the Borel measure 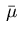 as in (4.10),
as in (4.10),
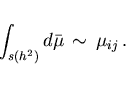 |
(4.21) |
from which we also get the special cases (4.11) and (4.12).
The situation is different for indices with either
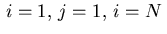 or
or 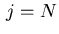 .
E.g., for indices
.
E.g., for indices
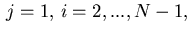 we get
we get
Note that this equation does not involve the variable 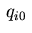 on the boundary.
Defining
on the boundary.
Defining 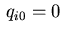 we arrive again at the discretized form of
the adjoint equation (3.6) using approximations as in
(4.10)-(4.12).
Similar relations hold for index combinations
we arrive again at the discretized form of
the adjoint equation (3.6) using approximations as in
(4.10)-(4.12).
Similar relations hold for index combinations
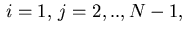 or
or
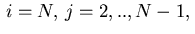 or
or
 .
For the remaining indices we find, e.g. for
.
For the remaining indices we find, e.g. for 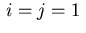 :
:
These relations do not involve the boundary variables 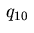 and
and
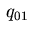 . Again, defining
. Again, defining 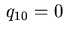 and
and 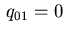 we recover the adjoint equations. In summary, by requiring the Dirichlet
boundary condition for the adjoint variables,
we recover the adjoint equations. In summary, by requiring the Dirichlet
boundary condition for the adjoint variables,
we see that the adjoint equation holds for all indices
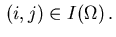
The necessary conditions with respect to the control variables 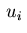 are determined for the indices
are determined for the indices
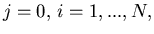 by
by
Observing 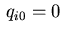 and
the approximation of the normal derivative in (4.4),
the minimum condition (3.8) holds with the identifications
and
the approximation of the normal derivative in (4.4),
the minimum condition (3.8) holds with the identifications
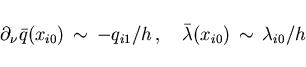 |
(4.22) |
Similar identifications hold for the other indices
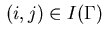 .
.


Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Neumann boundary conditions
Hans D. Mittelmann
2002-11-25
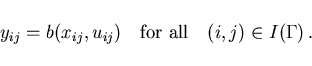
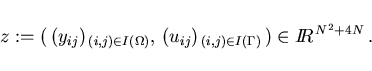
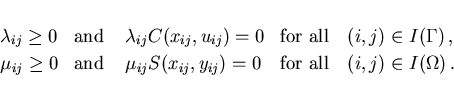
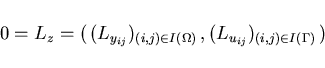
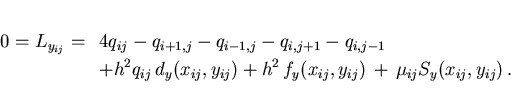
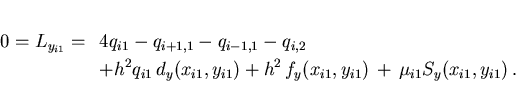
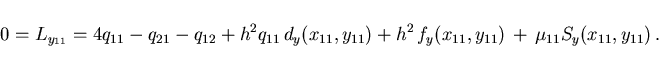
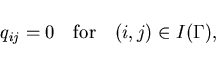
![]() are determined for the indices
are determined for the indices
![]() by
by
![\begin{eqnarray*}
0= L_{u_{i0}}
&& \hspace*{-5mm}
= h g_u(x_{i0},u_{i0}) - q_{i1...
...x_{i0},u_{i0}) +
\frac{\lambda_{i0}}{h}\,C_u(x_{i0},u_{i0})\,]
\end{eqnarray*}](img204.gif)