

Next: Numerical Verification
Up: paper94
Previous: Second order sufficient optimality
The test example
We fix here the following quantities in (P):
THEOREM 1
The quantities
satisfy the system of first order necessary conditions.
Proof
Insert the definitions above in the state equation and
adjoint equation. Then it is easy to check by elementary calculations that
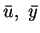 fulfill (1.2) and that
fulfill (1.2) and that 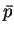 satisfies the
adjoint equation (2.2).
Moreover, the state-inequality constraint
(1.4) holds as an equality, since the integral of
satisfies the
adjoint equation (2.2).
Moreover, the state-inequality constraint
(1.4) holds as an equality, since the integral of 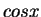 over
over
![$[0,\pi]$](img70.gif) vanishes. Clearly,
vanishes. Clearly, 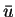 is an admissible control.
The variational inequality (2.3) is easy to verify by (2.5):
We find
is an admissible control.
The variational inequality (2.3) is easy to verify by (2.5):
We find
Therefore,
Next we consider the second order sufficient condition (SSC) for the example
analytically. What conditions must be checked to verify them? Thanks to our
construction, 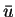 is strongly active on
is strongly active on 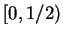 and
and 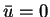 holds there.
If
holds there.
If 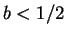 is given, then
is given, then
holds for ![$t \in [0,b]$](img77.gif) . Therefore,
. Therefore,
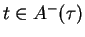 for
for
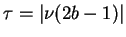 . To verify the second order sufficient conditions,
it suffices to confirm the coercivity condition (2.7) for all pairs
. To verify the second order sufficient conditions,
it suffices to confirm the coercivity condition (2.7) for all pairs
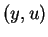 coupled through the linearized equation (2.8) and satisfying
coupled through the linearized equation (2.8) and satisfying
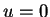 on
on ![$[0,b]$](img81.gif) (
(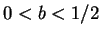 being arbitrary but fixed).
Assume that
being arbitrary but fixed).
Assume that
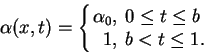 |
(3.1) |
THEOREM 2
Let
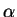
have the form (
3.1), where
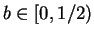
.
Then the second order sufficient conditions (SSC) are satisfied by
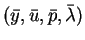
for arbitrary
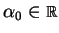
.
Proof
Let 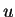 vanish on
vanish on ![$[0,b]$](img81.gif) and let
and let 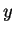 solve (2.8). Then
solve (2.8). Then 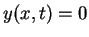 on
on ![$[0,b]$](img81.gif) . For
. For  we get
we get
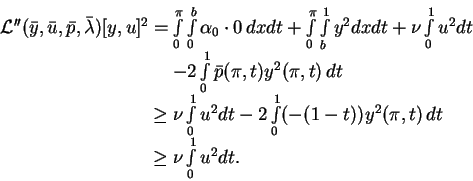 |
(3.2) |
Hence the coercivity condition (2.7) is satisfied.
Notice that 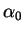 was not assumed to be positive. If
was not assumed to be positive. If 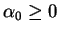 ,
then
,
then  is obviously coercive on the whole space
is obviously coercive on the whole space
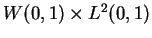 , and (SSC) is satisfied in a very strong sense. However, we might
find negative values for
, and (SSC) is satisfied in a very strong sense. However, we might
find negative values for 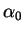 such that
such that 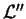 is partially
indefinite.
is partially
indefinite.
THEOREM 3
If
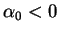
is sufficiently small, then a pair
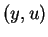
exists, such that
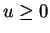
,
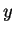
solves the linearized equation
(
2.8), and
![\begin{displaymath}
{\cal L''}(\bar{y},\bar{u},\bar{p},\bar{\lambda}) [y,u]^2 < 0.
\end{displaymath}](img95.gif) |
(3.3) |
Proof
We take an arbitrary but fixed 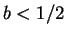 and set
and set
Then
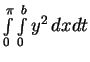 is positive. Hence
is positive. Hence
as
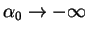 . Therefore, the expression
(3.2) becomes negative for sufficiently small
. Therefore, the expression
(3.2) becomes negative for sufficiently small 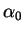 , if
, if
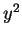 is substituted there for
is substituted there for 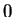 in the first integral.
in the first integral.
For the numerical verification we need a rough estimate on how small 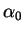 should be chosen. To get a negative value of
should be chosen. To get a negative value of
![${\cal L''}(\bar{y},\bar{u},\bar{p},\bar{\lambda}) [y,u]^2$](img101.gif) , we must have
, we must have
hence
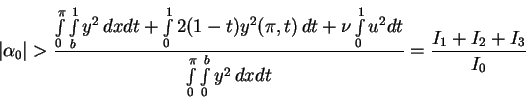 |
(3.4) |
must hold. Here, 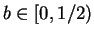 can be chosen arbitrarily.
We take the value
can be chosen arbitrarily.
We take the value 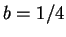 . Thus, we evaluate
the integrals
. Thus, we evaluate
the integrals 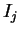 for
for
and the associated state 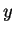 . The state
. The state 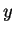 solves the homogeneous
heat equation subject to homogeneous initial condition, homogeneous
boundary condition at
solves the homogeneous
heat equation subject to homogeneous initial condition, homogeneous
boundary condition at 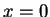 and
and
To avoid tedious estimates which might be performed by means of
a Fourier series representation of 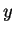 , we have evaluated the
integrals
, we have evaluated the
integrals 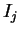 ,
, 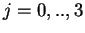 numerically. The result is
numerically. The result is
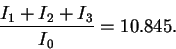 |
(3.5) |


Next: Numerical Verification
Up: paper94
Previous: Second order sufficient optimality
Hans D. Mittelmann
2003-01-25
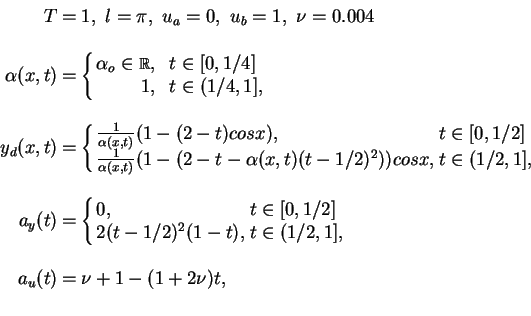
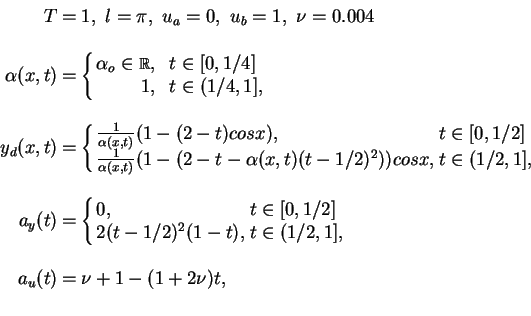
![\begin{displaymath}
\begin{array}{rcl}
e_Q(t) &=&\left\{
\begin{array}{ll}
0, & ...
.../2)^4- (2t-1), & t \in (1/2,1].
\end{array} \right.
\end{array}\end{displaymath}](img65.gif)
![]() fulfill (1.2) and that
fulfill (1.2) and that ![]() satisfies the
adjoint equation (2.2).
Moreover, the state-inequality constraint
(1.4) holds as an equality, since the integral of
satisfies the
adjoint equation (2.2).
Moreover, the state-inequality constraint
(1.4) holds as an equality, since the integral of ![]() over
over
![]() vanishes. Clearly,
vanishes. Clearly, ![]() is an admissible control.
The variational inequality (2.3) is easy to verify by (2.5):
We find
is an admissible control.
The variational inequality (2.3) is easy to verify by (2.5):
We find
![\begin{displaymath}
-1/\nu(\bar{p}(\pi,t) + a_u(t))= 2t-1=\left\{
\begin{array}{...
... 0, & t \in [0,1/2)\\
>0, & t \in (1/2,1].
\end{array}\right.
\end{displaymath}](img71.gif)
![]() is strongly active on
is strongly active on ![]() and
and ![]() holds there.
If
holds there.
If ![]() is given, then
is given, then
![]() vanish on
vanish on ![]() and let
and let ![]() solve (2.8). Then
solve (2.8). Then ![]() on
on ![]() . For
. For ![]() we get
we get
![]() was not assumed to be positive. If
was not assumed to be positive. If ![]() ,
then
,
then ![]() is obviously coercive on the whole space
is obviously coercive on the whole space
![]() , and (SSC) is satisfied in a very strong sense. However, we might
find negative values for
, and (SSC) is satisfied in a very strong sense. However, we might
find negative values for ![]() such that
such that ![]() is partially
indefinite.
is partially
indefinite.
![]() and set
and set
![\begin{displaymath}
u(t) = \left\{
\begin{array}{rl}
1 & \mbox{ on }[0,b]\\
0& \mbox{ on }(b,1].
\end{array}\right.
\end{displaymath}](img96.gif)
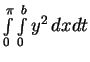 is positive. Hence
is positive. Hence
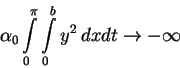
![]() should be chosen. To get a negative value of
should be chosen. To get a negative value of
![]() , we must have
, we must have
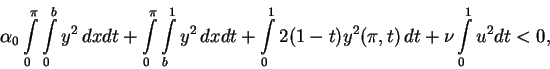
![\begin{displaymath}
u(t)= \left\{
\begin{array}{rl}
1& \, \mbox{ on }[0,1/4]\\
0& \, \mbox{ on }(1/4,1]
\end{array} \right.
\end{displaymath}](img106.gif)
![\begin{displaymath}
y_x(\pi,t)= \left\{
\begin{array}{ll}
1& \, \mbox{ on }[0,1/...
...
-2 \bar{y}(\pi,t)& \, \mbox{ on }(1/4,1].
\end{array} \right.
\end{displaymath}](img108.gif)