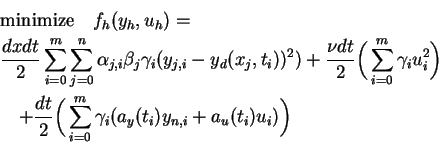
In this section it is our goal to first demonstrate that problem (P) can be solved to good accuracy using a finite difference method. Next, as was done in [7,8] we will, through an eigenvalue computation, verify that the computed solution satisfies the SSC and is thus a local minimizer. Then, in order to check the properties of the specific example shown analytically above, we will compute an additional eigenvalue. We start by presenting the finite-dimensional analogue of (P) and then outline how the algebraic problems are solved. We define the following discretization of problem (P).
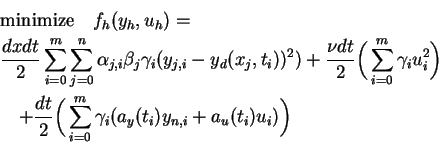
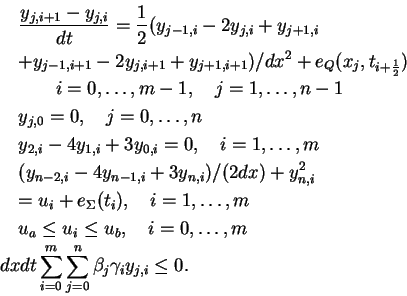
The discrete control problem (P![]() ) is essentially a generic nonlinear
optimization problem of the form
) is essentially a generic nonlinear
optimization problem of the form
No Hessian of ![]() appears on the right due to its linearity.
To clarify the relationship between the way we proceed here and which
is standard in optimization and the analysis of the previous section
we add the following explanations. In order to verify the SSC in the
discrete case we have to determine the smallest eigenvalue of the
Hessian on the tangent space of the active constraints. We do this by
explicitly computing the orthogonal projection matrix
appears on the right due to its linearity.
To clarify the relationship between the way we proceed here and which
is standard in optimization and the analysis of the previous section
we add the following explanations. In order to verify the SSC in the
discrete case we have to determine the smallest eigenvalue of the
Hessian on the tangent space of the active constraints. We do this by
explicitly computing the orthogonal projection matrix ![]() onto the
tangent space and forming
onto the
tangent space and forming ![]() . Due to the verified regularity
of the computed solution or the nondegeneracy of the active constraints
the tangent space is equal to the nullspace of the active constraint
gradients and thus the smallest eigenvalue of
. Due to the verified regularity
of the computed solution or the nondegeneracy of the active constraints
the tangent space is equal to the nullspace of the active constraint
gradients and thus the smallest eigenvalue of ![]() corresponds
to the minimal value of its quadratic form on the space of all
corresponds
to the minimal value of its quadratic form on the space of all ![]() satisfying the linearized equation as well as having vanishing
satisfying the linearized equation as well as having vanishing ![]() components corresponding to indices
components corresponding to indices ![]() for which the solution is
at the bound which coincidentally also is zero. These components do
include the ones corresponding to the interval
for which the solution is
at the bound which coincidentally also is zero. These components do
include the ones corresponding to the interval ![]() .
Next, we will detail how condition (4.2) will be checked.
.
Next, we will detail how condition (4.2) will be checked.
As was already done in [7,8] the control problems are written in the form of AMPL [6] scripts. This way, a number of nonlinear optimization codes can be utilized for their solution. It had been an observation in our previous work that from the then available codes only LOQO [14] was able to solve all the problems effectively and for sufficiently fine discretizations. This has changed. As recent comparisons [9] have shown, the trust region interior point method KNITRO [2] which became available only recently, may outperform LOQO on such problems. It was used for the computations reported below. The following procedure is independent of the solver used.
After computing a solution an AMPL stub (or ![]() ) file is written
as well as a file with the computed Lagrange multipliers. This allows to
check the SSC (4.2) with the help of a Fortran, alternatively, a C
or Matlab, program.
This program reads the files and verifies first the necessary first-order
optimality conditions, the column regularity of
) file is written
as well as a file with the computed Lagrange multipliers. This allows to
check the SSC (4.2) with the help of a Fortran, alternatively, a C
or Matlab, program.
This program reads the files and verifies first the necessary first-order
optimality conditions, the column regularity of ![]() and the strict
complementarity. For this, it utilizes routines provided by AMPL which
permit evaluation of the objective and constraint gradients. Next, the
the QR decomposition of
and the strict
complementarity. For this, it utilizes routines provided by AMPL which
permit evaluation of the objective and constraint gradients. Next, the
the QR decomposition of ![]() is computed by one of the methods
exploiting sparsity. We have utilized the algorithm described in [12].
AMPL also provides a routine to multiply the Hessian of the Lagrangian times a
vector. This is called with the columns of
is computed by one of the methods
exploiting sparsity. We have utilized the algorithm described in [12].
AMPL also provides a routine to multiply the Hessian of the Lagrangian times a
vector. This is called with the columns of ![]() and thus
and thus ![]() can be
formed. Its eigenvalues are computed with LAPACK routine DSYEV and the
smallest eigenvalue
can be
formed. Its eigenvalues are computed with LAPACK routine DSYEV and the
smallest eigenvalue
![]() is determined.
The use of this eigenvalue routine is possible since the order of the
matrices corresponding to the "free" control variables is moderate. In
case of distributed control problems when this number may be on the order
of the state variables, a sparse solver, preferably just for finding the
minimal eigenvalue, will have to be used.
is determined.
The use of this eigenvalue routine is possible since the order of the
matrices corresponding to the "free" control variables is moderate. In
case of distributed control problems when this number may be on the order
of the state variables, a sparse solver, preferably just for finding the
minimal eigenvalue, will have to be used.
With the procedure described above the SSC for problem (P![]() ) can be
checked for constant or variable
) can be
checked for constant or variable ![]() . In the nonconstant case
and for
. In the nonconstant case
and for ![]() below the bound given above an additional eigenvalue
problem is solved. Let
below the bound given above an additional eigenvalue
problem is solved. Let ![]() in the previous section be split into
in the previous section be split into
![]() where now
where now ![]() corresponds to the equality
constraints only and thus has
corresponds to the equality
constraints only and thus has ![]() columns. Then, in analogy to (4.2)
we define
columns. Then, in analogy to (4.2)
we define ![]() and call its smallest (leftmost on the real
line) eigenvalue
and call its smallest (leftmost on the real
line) eigenvalue ![]() . We will have to obtain a negative
. We will have to obtain a negative
![]() for sufficiently negative
for sufficiently negative ![]() .
As described above, this
.
As described above, this ![]() projects onto the nullspace of the equality
constraints only and thus
projects onto the nullspace of the equality
constraints only and thus ![]() is the projection of the Hessian onto
the larger subspace of pairs
is the projection of the Hessian onto
the larger subspace of pairs ![]() satisfying the linearized equation
only and for which
satisfying the linearized equation
only and for which ![]() may be nonzero everywhere on
may be nonzero everywhere on ![]() .
.
Problem (4.2) was solved as described above for two discretizations which were chosen to be about equidistant in both coordinates. In Table 1 are the errors of both state and control listed in two different norms.
|