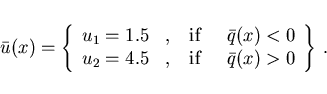

Next: Example 3
Up: Numerical examples
Previous: Example 1
We choose  in Example 1 and expect to
obtain a bang-bang control.
The adjoint equation agrees with that in (4.1).
In view of
in Example 1 and expect to
obtain a bang-bang control.
The adjoint equation agrees with that in (4.1).
In view of 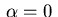 the control law (2.22) yields
the control law (2.22) yields
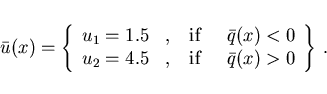 |
(4.3) |
Table 2:
Information on solution of Example 2
| N+1 |
it |
CPU |
Acc |
 |
| 50 |
30 |
112 |
8 |
.0521138 |
| 100 |
37 |
2169 |
8 |
.0564474 |
| 200 |
45 |
67769 |
8 |
.0596968 |
|
Figure 3 shows that the optimal control is indeed bang-bang and does not
exhibit singular parts.
The optimal state and adjoint variables are displayed in
Figure 4. Both figures allow to verify precisely the switching conditions
of the control law (4.3).
Hans D. Mittelmann
2000-10-06