

Next: Discretization and optimization techniques
Up: paper
Previous: Introduction
Necessary conditions for elliptic control problems
with control and state constraints
Let
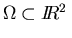 be a bounded domain
with piecewise smooth boundary
be a bounded domain
with piecewise smooth boundary
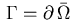 .
The derivative in the direction of the outward unit normal
.
The derivative in the direction of the outward unit normal 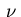 of
of
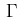 will be denoted by
will be denoted by
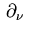 .
Suppose that the boundary is partioned as
.
Suppose that the boundary is partioned as
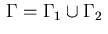 with disjoints sets
with disjoints sets
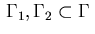 that are composed of finitely
many smooth and connected components.
that are composed of finitely
many smooth and connected components.
We consider the optimal control problem of determining a
distributed control function
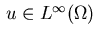 that minimizes the functional
that minimizes the functional
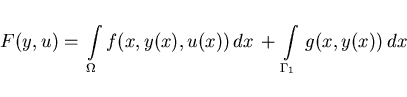 |
(2.1) |
subject to the elliptic state equation,
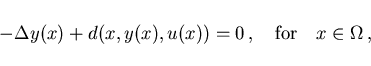 |
(2.2) |
Neumann and Dirichlet boundary conditions,
and mixed control-state inequality constraints, resp. pure
state inequality constraints,
| |
|
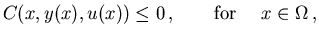 |
(2.5) |
| |
|
 |
(2.6) |
The split boundary formulation permits simultaneous treatment of
various boundary conditions while in [23] this was done in
separate sections.
The functions
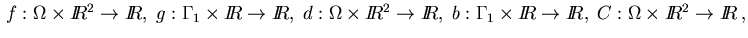 and
and
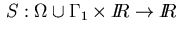 are supposed to be
are supposed to be  -functions and
-functions and
 is assumed in the Dirichlet condition (2.4).
We have to admit that no numerical example with a spliting of the boundary
is assumed in the Dirichlet condition (2.4).
We have to admit that no numerical example with a spliting of the boundary
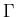 into
into
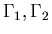 will be considered in this paper.
However, the spltting has been introduced to allow for a general discussion
of necessary conditions. A practical example with splitted boundary may
be found in [25].
will be considered in this paper.
However, the spltting has been introduced to allow for a general discussion
of necessary conditions. A practical example with splitted boundary may
be found in [25].
The Laplacian
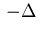 in the elliptic equation (2.2)
can be replaced by an elliptic operator
in the elliptic equation (2.2)
can be replaced by an elliptic operator 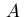 in divergence form.
We refer to section 2 of [23] for a precise definition.
The above distributed control problem is slightly more general than the one
considered in Bonnans and Casas [6] where first order
conditions have been given in terms of a weak and strong Pontryagin principle.
For linear elliptic equations, first order conditions may also
be found in Bergounioux et al. [3], Bonnans and Casas
[5].
Nonlinear elliptic equations of Lotka-Volterra type have been considered in
Cañada et al. [8] and Leung, Stojanovic [21,28].
in divergence form.
We refer to section 2 of [23] for a precise definition.
The above distributed control problem is slightly more general than the one
considered in Bonnans and Casas [6] where first order
conditions have been given in terms of a weak and strong Pontryagin principle.
For linear elliptic equations, first order conditions may also
be found in Bergounioux et al. [3], Bonnans and Casas
[5].
Nonlinear elliptic equations of Lotka-Volterra type have been considered in
Cañada et al. [8] and Leung, Stojanovic [21,28].
Throughout this paper, it wil be assumed that an optimal solution
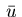 and
and 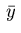 of problem (2.1)-(2.6) exists.
To ensure well-posedness of the elliptic problem
(2.1)-(2.3) we require as in Bonnans, Casas [6], condition (2.3), that
of problem (2.1)-(2.6) exists.
To ensure well-posedness of the elliptic problem
(2.1)-(2.3) we require as in Bonnans, Casas [6], condition (2.3), that
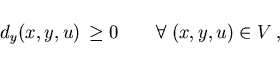 |
(2.7) |
holds where 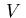 is a suitable bounded set containing the graph
of the optimal solution.
In special cases, such as Examples 1 and 2 below, one can dispense with
this condition since well-posedness follows from special results
cf. Gunzburger et al. [15].
However, we should note that condition (2.7) is not
satisfied for all numerical examples in section 4.
is a suitable bounded set containing the graph
of the optimal solution.
In special cases, such as Examples 1 and 2 below, one can dispense with
this condition since well-posedness follows from special results
cf. Gunzburger et al. [15].
However, we should note that condition (2.7) is not
satisfied for all numerical examples in section 4.
The active sets for the inequality constraints
(2.5), (2.6) are given by
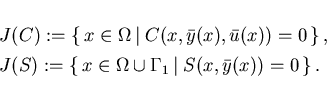 |
(2.8) |
We do not study regularity conditions in detail and require that
the following ones
hold:
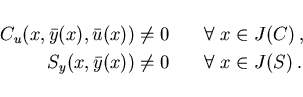 |
(2.9) |
Extending in a purely formal way the first order necessary conditions
in Bonnans and Casas [6], we arrive at the following.
There exists an adjoint state
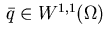 ,
a multiplier
,
a multiplier
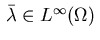 ,
and a regular Borel measure
,
and a regular Borel measure
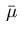 in
in 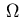 such that the following conditions hold:
such that the following conditions hold:
adjoint equation and boundary conditions:
minimum condition for
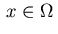 :
:
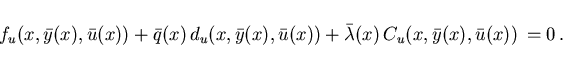 |
(2.13) |
complementarity conditions:
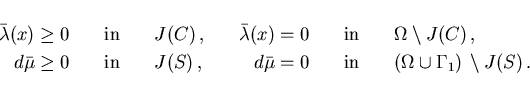 |
(2.14) |
The adjoint equations (2.10)-(2.12) are understood
in the weak sense.
According to Bourbaki [7], Chapter 9,
the regular Borel measure in the adjoint equations (2.10) and
(2.11) possesses a decomposition
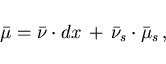 |
(2.15) |
where 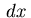 represents the Lebesgue measure, the measure
represents the Lebesgue measure, the measure
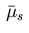 is singular with respect to
is singular with respect to 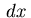 and
and
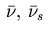 are measurable.
are measurable.
In many applications, the control and state constraints (2.5) and (2.6) are simple box constraints of the type
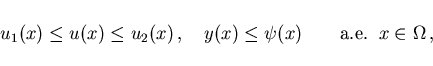 |
(2.16) |
with functions
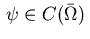 and
and
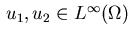 .
In this case, the adjoint equation (2.10) reduces to
.
In this case, the adjoint equation (2.10) reduces to
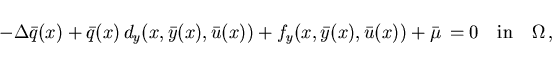 |
(2.17) |
while the the minimum condition (2.13) yields the control law
![\begin{displaymath}
\begin{array}{l}
[\,f_u(x,\bar{y}(x),\bar{u}(x)) + \bar{q}(x...
...ll \; u \in [u_1(x),u_2(x)] \,, \; x \in \Omega \,.
\end{array}\end{displaymath}](img58.gif) |
(2.18) |
A further specialization refers to a cost functional (2.1) of
tracking type which has been considered frequently, cf. [1,2,19,20],
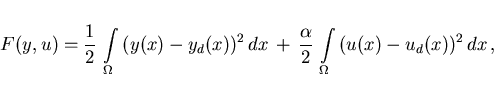 |
(2.19) |
with given functions
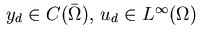 ,
and a nonnegative weight
,
and a nonnegative weight
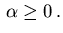 Furthermore, let the function
Furthermore, let the function 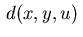 in the
state equation (2.2) be linear in the control variable with
in the
state equation (2.2) be linear in the control variable with
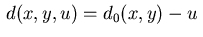 .
Then we deduce from (2.18) the minimum condition
.
Then we deduce from (2.18) the minimum condition
![\begin{displaymath}
\hspace*{-8mm}
[\alpha (\bar{u}(x)-u_d(x)) - \bar{q}(x)] \, ...
... \; u \in [u_1(x),u_2(x)]\,, \; \mbox{a.e. in }
\Omega \, . \;
\end{displaymath}](img64.gif) |
(2.20) |
Case
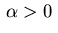 : The previous conditions show that the optimal
control
: The previous conditions show that the optimal
control
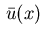 is the projection of
is the projection of
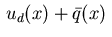 onto the interval
onto the interval
![$\,[u_1(x),u_2(x)]\,$](img68.gif) .
More precisely, we have for
.
More precisely, we have for
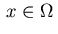 :
:
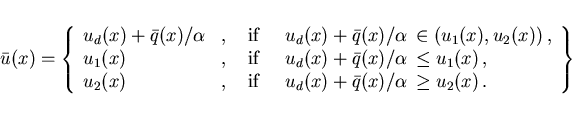 |
(2.21) |
Case 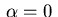 : We obtain an optimal control of
bang-bang or singular type,
: We obtain an optimal control of
bang-bang or singular type,
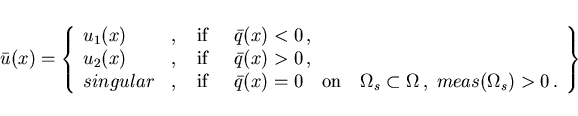 |
(2.22) |


Next: Discretization and optimization techniques
Up: paper
Previous: Introduction
Hans D. Mittelmann
2000-10-06
![]() that minimizes the functional
that minimizes the functional
![]() in the elliptic equation (2.2)
can be replaced by an elliptic operator
in the elliptic equation (2.2)
can be replaced by an elliptic operator ![]() in divergence form.
We refer to section 2 of [23] for a precise definition.
The above distributed control problem is slightly more general than the one
considered in Bonnans and Casas [6] where first order
conditions have been given in terms of a weak and strong Pontryagin principle.
For linear elliptic equations, first order conditions may also
be found in Bergounioux et al. [3], Bonnans and Casas
[5].
Nonlinear elliptic equations of Lotka-Volterra type have been considered in
Cañada et al. [8] and Leung, Stojanovic [21,28].
in divergence form.
We refer to section 2 of [23] for a precise definition.
The above distributed control problem is slightly more general than the one
considered in Bonnans and Casas [6] where first order
conditions have been given in terms of a weak and strong Pontryagin principle.
For linear elliptic equations, first order conditions may also
be found in Bergounioux et al. [3], Bonnans and Casas
[5].
Nonlinear elliptic equations of Lotka-Volterra type have been considered in
Cañada et al. [8] and Leung, Stojanovic [21,28].
![]() and
and ![]() of problem (2.1)-(2.6) exists.
To ensure well-posedness of the elliptic problem
(2.1)-(2.3) we require as in Bonnans, Casas [6], condition (2.3), that
of problem (2.1)-(2.6) exists.
To ensure well-posedness of the elliptic problem
(2.1)-(2.3) we require as in Bonnans, Casas [6], condition (2.3), that