Discretization and optimization techniques

The discussion of discretization schemes is restricted to the standard situation where the elliptic operator is the Laplacian $\,A=-\Delta\,$ and the domain is the unit square $\,\Omega=(0,1)\times (0,1)\,.$ The generalization to a general elliptic operator is straightforward. However, the modifications for an arbitrary domain $\,\Omega\,$ depend essentially on the geometry of the boundary $\,\Gamma\,$.

The purpose of this section is to develop discretization techniques by which the problem (2.1)-(2.4) with Neumann boundary conditions resp. problem (3.1)-(3.4) with Dirichlet boundary conditions is transformed into a nonlinear programming problem (NLP-problem) of the form

$$\begin{array}{ll} \mbox{Minimize} & F^h(z) \\ \mbox{subject to} & G^h(z) = 0 \,, \quad H(z) \leq 0 \,. \end{array}$$ (4.1)

The functions $\,F^h, G^h\,$ and $\,H\,$ are sufficiently smooth and of appropriate dimension. The upper subscript $\,h\,$ denotes the dependence on the stepsize. The optimization variable $\,z\,$ will comprise both the state and the control variables.

The form (4.1) will be achieved by solving the elliptic equation (2.2) with the standard five-point-star discretization scheme. Choose a number $\,N \in I\!\!N_+\,$ and the stepsize $\,h:=1/(N+1)\,.$ Consider the mesh points

$$\,x_{ij}=(ih,jh)\,, \quad 0 \leq i,j \leq N+1, \,$$

and consider the following sets of indices $\,(i,j)\,$ residing either in the domain $\,\Omega\,$ or on the four edges of the boundary $\,\Gamma\,$:

$$\begin{array}{l} I(\Omega):=\{\,(i,j)\, \vert \; 1 \leq i,j ... ...mm] I(\bar{\Omega}): = I(\Omega) \cup I(\Gamma) \,. \end{array}$$ (4.2)

We have $\;\char93 I(\Omega)= N^2\,$ and $\;\char93 I(\Gamma)= 4*N\,$. Denote approximations for the values $\,y(x_{ij})\,$ of the state variables by $\,y_{ij} \,$ for $\,(i,j) \in I(\bar{\Omega})\,$ and denote approximations of the values $\,u(x_{ij})\,$ of the control variables by $\,u_{ij}\,$ for $\,(i,j) \in I(\Gamma)\,$.

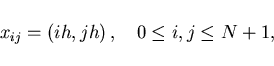
Now we shall specify the functions $\,F^h, G^h, H\,$ for the optimization problem (4.1) both for Neumann and Dirichlet boundary conditions.