

Next: Elliptic control problems with
Up: paper84
Previous: Introduction
Elliptic control problems with Neumann boundary conditions
The following elliptic control problem with control and state constraints
constitutes a generalization of elliptic problems considered in
Casas [9], Casas et al. [10,11],
Ito, Kunisch [16], Kunisch, Volkwein [18].
The problem is to determine a control
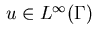 that minimizes the functional
that minimizes the functional
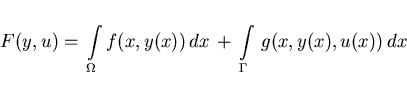 |
(2.1) |
subject to the state equation
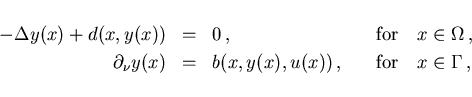 |
(2.2) |
and the inequality constraints on control and state
| |
|
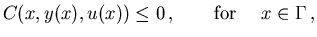 |
(2.3) |
| |
|
 |
(2.4) |
In this setting,
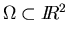 is a bounded domain
with piecewise smooth boundary
is a bounded domain
with piecewise smooth boundary
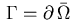 .
The derivative in the direction of the outward unit normal
.
The derivative in the direction of the outward unit normal 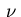 of
of
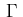 is denoted by
is denoted by
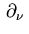 in (2.2).
Note that the state inequality constraints (2.4) are supposed
to hold on the closure of
in (2.2).
Note that the state inequality constraints (2.4) are supposed
to hold on the closure of 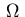 .
.
The Laplacian 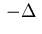 in (2.2)
can be replaced by an elliptic operator
in (2.2)
can be replaced by an elliptic operator
where the coefficients
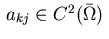 satisfy the
following coercivity condition with some
satisfy the
following coercivity condition with some 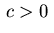 :
:
However, in the sequel we restrict the discussion to the operator
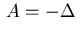 which simplifies the form of the necessary conditions
and the presentation of the numerical approach in section 4.
The functions
which simplifies the form of the necessary conditions
and the presentation of the numerical approach in section 4.
The functions
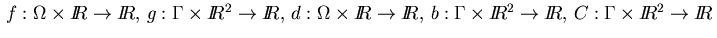 and
and
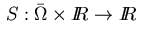 are assumed to be
are assumed to be 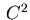 -functions. It is straightforward to include more than one inequality constraint into (2.3) or (2.4).
However, since both the state and control variable are scalar variables,
the active sets for different inequality constraints are disjoint and
hence can be treated separately.
-functions. It is straightforward to include more than one inequality constraint into (2.3) or (2.4).
However, since both the state and control variable are scalar variables,
the active sets for different inequality constraints are disjoint and
hence can be treated separately.
Then under appropriate assumptions on the function 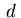 it can be shown that the state equation (2.2) admits for each
it can be shown that the state equation (2.2) admits for each
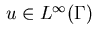 a weak solution
a weak solution
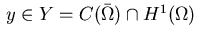 (cf. Casas et al. [10]), i.e., it holds
(cf. Casas et al. [10]), i.e., it holds
for all
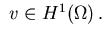 An optimal solution of problem (2.1)-(2.4) will be
denoted by
An optimal solution of problem (2.1)-(2.4) will be
denoted by 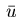 and
and 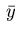 .
From [10] we infer the further assumption that the function
.
From [10] we infer the further assumption that the function 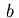 in the Neumann condition (2.2) is sufficiently smooth and
satisfies the following inequality with suitable
in the Neumann condition (2.2) is sufficiently smooth and
satisfies the following inequality with suitable
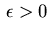 ,
,
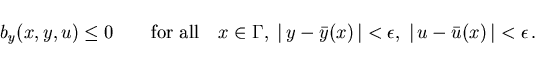 |
(2.5) |
Questions of existence of optimal
solutions will not be discussed here.
The active sets for the inequality constraints (2.3) and (2.4) are defined by
It is required that the following regularity conditions hold:
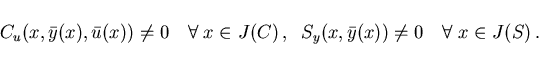 |
(2.6) |
Here and in the following, partial derivatives are denoted by subscripts.
First order optimality conditions for a local optimal solution
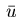 and
and 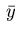 can be derived by generalizing the line of
proof in Casas [9], Casas et al. [10,11].
Problem (2.1)-(2.4) is considered
as a mathematical programming problem in Banach spaces to which the first
order Kuhn-Tucker conditions are applicable.
In particular, this approach requires that the regularity condition given
in Zowe, Kurcyusz [24] is satisfied;
cf. Casas et al. [11].
We do not discuss this regularity condition in detail although
condition (2.6) forms part of it.
The first order necessary conditions imply that there exist an
adjoint state
can be derived by generalizing the line of
proof in Casas [9], Casas et al. [10,11].
Problem (2.1)-(2.4) is considered
as a mathematical programming problem in Banach spaces to which the first
order Kuhn-Tucker conditions are applicable.
In particular, this approach requires that the regularity condition given
in Zowe, Kurcyusz [24] is satisfied;
cf. Casas et al. [11].
We do not discuss this regularity condition in detail although
condition (2.6) forms part of it.
The first order necessary conditions imply that there exist an
adjoint state
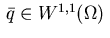 ,
a multiplier
,
a multiplier
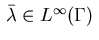 ,
and a bounded Borel measure
,
and a bounded Borel measure 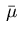 on
on
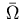 such that the following three conditions hold,
such that the following three conditions hold,
1. adjoint equation:
2. minimum condition on 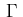 :
:
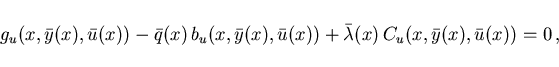 |
(2.9) |
3. complementarity condition:
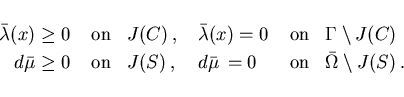 |
(2.10) |
The adjoint equations (2.7), (2.8) are understood
in the weak sense, cf. Casas et al. [11].
According to Bourbaki [6], Chapter 9, the bounded Borel measure
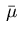 appearing in the adjoint equation (2.7), (2.8)
has the decomposition
appearing in the adjoint equation (2.7), (2.8)
has the decomposition
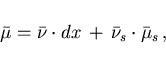 |
(2.11) |
where 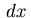 represents the Lebesgue measure and
represents the Lebesgue measure and
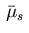 is singular
with respect to
is singular
with respect to 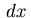 ; the functions
; the functions
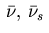 are
measurable on
are
measurable on
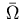 .
The problem of obtaining the decomposition (2.11) explicitly
is related to the difficulty of determining the structure of the active set
.
The problem of obtaining the decomposition (2.11) explicitly
is related to the difficulty of determining the structure of the active set
 .
To our knowledge, the literature does not contain any numerical examples
where the decomposition (2.11) has actually been computed.
In section 4, we shall make an attempt to approximate the measure by the
multipliers of the discretized problem.
.
To our knowledge, the literature does not contain any numerical examples
where the decomposition (2.11) has actually been computed.
In section 4, we shall make an attempt to approximate the measure by the
multipliers of the discretized problem.
In later applications, we shall mostly deal with cost functionals of
tracking type (cf. Ito, Kunisch [16]),
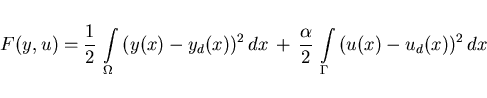 |
(2.12) |
with given functions
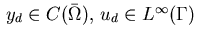 ,
and a nonnegative weight
,
and a nonnegative weight
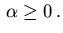 The control and state constraints (2.3) and (2.4)
are supposed to be box constraints of the simple type
The control and state constraints (2.3) and (2.4)
are supposed to be box constraints of the simple type
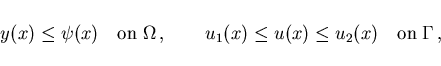 |
(2.13) |
with functions
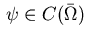 and
and
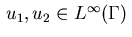 .
For these data the adjoint equation (2.7), (2.8) become
.
For these data the adjoint equation (2.7), (2.8) become
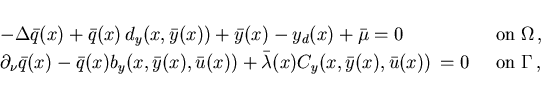 |
(2.14) |
If the function 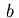 in (2.2) has the form
in (2.2) has the form
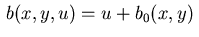 , i.e., if
, i.e., if
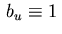 holds,
then the minimum condition (2.9) reduces to
holds,
then the minimum condition (2.9) reduces to
![\begin{displaymath}
\hspace*{-10mm}
[\alpha (\bar{u}(x)-u_d(x)) - \bar{q}(x)] \,...
...\quad \forall \, x \in \Gamma, \; u \in [u_1(x),u_2(x)] \,. \;
\end{displaymath}](img58.gif) |
(2.15) |
Case
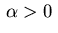 : condition (2.15) shows that the control
: condition (2.15) shows that the control
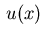 is given by the projection of
is given by the projection of
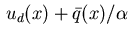 on the interval
on the interval
![$\,[u_1(x),u_2(x)]\,$](img62.gif) which can be stated more explicitly as
which can be stated more explicitly as
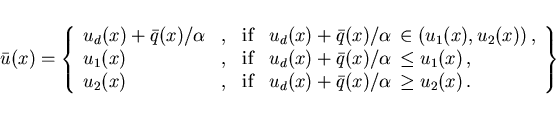 |
(2.16) |
Case 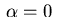 : we obtain an optimal control of bang-bang
or singular type:
: we obtain an optimal control of bang-bang
or singular type:
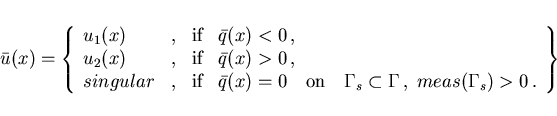 |
(2.17) |
Thus, for 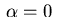 the adjoint function
the adjoint function
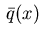 on the boundary
plays the role of a switching function. The isolated zeros of
on the boundary
plays the role of a switching function. The isolated zeros of
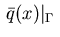 are the switching points of a bang-bang control.
are the switching points of a bang-bang control.


Next: Elliptic control problems with
Up: paper84
Previous: Introduction
Hans D. Mittelmann
2002-11-25
![]() that minimizes the functional
that minimizes the functional
![]() in (2.2)
can be replaced by an elliptic operator
in (2.2)
can be replaced by an elliptic operator
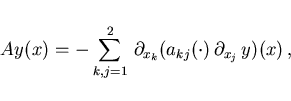
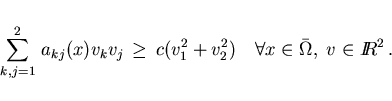
![]() it can be shown that the state equation (2.2) admits for each
it can be shown that the state equation (2.2) admits for each
![]() a weak solution
a weak solution
![]() (cf. Casas et al. [10]), i.e., it holds
(cf. Casas et al. [10]), i.e., it holds
![\begin{displaymath}
\int \limits_{\Omega} \, [\,\Delta y(x)\,\Delta v(x) + d(x,y...
...v(x)\,]\,dx =
\int \limits_{\Gamma}\,b(x,y(x),u(x))\,v(x)\,dx
\end{displaymath}](img24.gif)
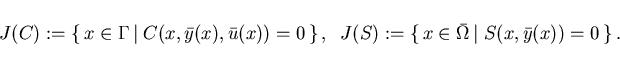
![]() and
and ![]() can be derived by generalizing the line of
proof in Casas [9], Casas et al. [10,11].
Problem (2.1)-(2.4) is considered
as a mathematical programming problem in Banach spaces to which the first
order Kuhn-Tucker conditions are applicable.
In particular, this approach requires that the regularity condition given
in Zowe, Kurcyusz [24] is satisfied;
cf. Casas et al. [11].
We do not discuss this regularity condition in detail although
condition (2.6) forms part of it.
The first order necessary conditions imply that there exist an
adjoint state
can be derived by generalizing the line of
proof in Casas [9], Casas et al. [10,11].
Problem (2.1)-(2.4) is considered
as a mathematical programming problem in Banach spaces to which the first
order Kuhn-Tucker conditions are applicable.
In particular, this approach requires that the regularity condition given
in Zowe, Kurcyusz [24] is satisfied;
cf. Casas et al. [11].
We do not discuss this regularity condition in detail although
condition (2.6) forms part of it.
The first order necessary conditions imply that there exist an
adjoint state
![]() ,
a multiplier
,
a multiplier
![]() ,
and a bounded Borel measure
,
and a bounded Borel measure ![]() on
on
![]() such that the following three conditions hold,
such that the following three conditions hold,