Predictor-Corrector Algorithms

The predictor-corrector method for linear programming was proposed by Mehrotra [6] based on a second-order correction to the pure Newton direction. This method works quite well for LP and QP in practice, although its theoretical result in [18] has the same complexity as the short-step method. In this section we start by describing the idea of the predictor-corrector method and then derive its linear system for SOCP and give two variants of the algorithm.

Given a point $(x,\tau,y,s,\kappa)$ with $(x,\tau),(s,\kappa)\in\bar{K}.$ The predictor direction is found by solving the following system:

$$\begin{pmatrix}A&-b&0&0&0\cr 0&-c&A^T&I&0\cr -c^T&0&b^T&0&-1\cr \... ...n{pmatrix}-r_1\cr -r_2\cr -r_3\cr -\bar{X}\bar{S}e\cr -\tau\kappa\end{pmatrix},$$ (4-4)

where $r_1, r_2,r_3$ are defined as in (4-3). Next, we find the step length $\alpha_p$ along this direction:

$$\alpha_p= \{\alpha\in [0,1]\Vert(x,\tau)+\alpha(\triangle x_p,\triangle\tau_p),(s,\kappa)+\alpha(\triangle s_p,\triangle\kappa_p)\in\bar{K}\},$$ (4-5)

and define

$$\mu_p=[(x+\alpha_p\triangle x_p)^T(s+\alpha_p\triangle s_p)+(\tau+\alpha_p\triangle\tau_p)(\kappa+\alpha_p\triangle\kappa_p)]/(k+1).$$ (4-6)

Note that the reduction obtained using the predictor is larger than that for the long-step path-following method since

$$\begin{array}{rcl} (x+\triangle x_p)^T(s+\triangle s_p)&=&x^... ...p\\ & <&\triangle x_p^T\triangle s_p+\sigma\mu e. \end{array}$$

We now consider the corrector direction and the centralizing step at once. Denote a corrector-centering step by $(\triangle x_c,\triangle\tau_c,\triangle y_c,\triangle s_c,\triangle\kappa_c).$ Assuming that the full step of predictor and corrector-centering directions are taken, we expect

$$(x^i+\triangle x^i_p+\triangle x^i_c)^T(s^i+\triangle s^i_p+\triangle s^i_c)=\sigma\mu, i=1:k.$$ (4-7)

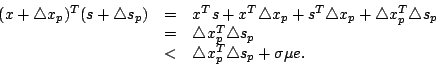
After expanding the left hand side of (4-7) and ignoring the higher order terms $(\triangle x^i_p)^T\triangle s^i_c,$ $(\triangle s^i_p)^T\triangle x^i_c,$ and $(\triangle x^i_c)^T\triangle s^i_c$, one has

$$(s^i)^T\triangle x^i_c+(x^i)^T\triangle s^i_c\approx\sigma\mu -(\triangle x^i_p)^T\triangle s^i_p.$$

Then, the corrector-centering direction is obtained by solving

$$\begin{pmatrix}A&-b&0&0&0\cr 0&-c&A^T&I&0\cr -c^T&0&b^T&0&-1\cr \... ...riangle\bar{S_p}e\cr \sigma\mu_p-\triangle\tau_p\triangle\kappa_p\end{pmatrix}.$$ (4-8)

We describe two algorithms using the predictor direction and the corrector-centering direction mentioned above. All initial data are chosen as in Algorithm4.2.

Algorithm 4.4   Initial Data as in Algorithm 4.2

$$% latex2html id marker 4253\begin{array}{rl} \mbox{Let}& \... ...)=\phi +\alpha_{max}\triangle \phi\\ \mbox{end.}& \end{array}$$

Algorithm 4.5   Initial Data as in Algorithm 4.2

$$% latex2html id marker 4257 \begin{array}{rl} \mbox{Let}& \c... ...=\phi+ \triangle\phi(\alpha_{max})\\ \mbox{end.}& \end{array}$$

Table 2 lists the results for these algorithms as well as for the long-step path-following method, i.e., Algorithm 4.2 combined with Algorithm 4.3 and it compares those with all four algorithms for SOCP problems we had evaluated for the Seventh DIMACS implementation Challenge [7]. Similar to LP, Table 2 also shows that in our test case Mehrotra's version of the predictor-corrector method works better than long-step path-following methods. Moreover, the quadratic combination of predictor and corrector directions, i.e., Algorithm 4.5, has a few great results, but it is still worse than Algorithm 4.4 overall, sometimes even worse than the long-step algorithm. Besides the above two algorithms, we would have two variants for Algorithm 4.4. First, inspired by [3,8], we implemented a code for the inexact Newton method by adding a small residual term to the right hand side. We use inexact_pc to denote this algorithm. Second, using the predictor direction one more time if the reduction of $\mu$ is significant. We denote this method as ppc. Moreover, instead of solving the full system, we use the normal equations in Table 3. In order to solve large scale problems, solving the full linear system is not as efficient as solving the normal equations. Nevertheless, for some problems, the condition number of the coefficient matrix for the normal equations is much larger than for the full linear system as the point is getting closer to the solution, for example, EX2-75 (see Figure 2).

Table 2: Comparison of our methods with the codes [1,12,14,15]

	A. 4.4	A. 4.5	A.4.2	SeDu	SDPT	MOSK	LOQO
EX1-50	13	15	20	13	12	13	44
EX1-75	16	14	21	16	11	13	44
EX1-100	14	16	22	16	12	14	51
EX1-200	17	17	23	16	12	16	60
EX2-50	9	10	13	15	9	8	13
EX2-100	8	13	13	12	10	8	14
EX2-150	9	9	14	15	10	10	12
EX2-200	10	9	14	14	10	10	13
EX3-10-4	13	14	18	13	21	10	88
EX3-20-4	11	13	16	14	16	10	f
EX3-30-9	11	14	18	14	15	10	f
EX3-40-9	13	14	18	14	12	10	f
EX4-mark	12	14	18	10	na	9	na
EX4-return	15	14	23	12	na	9	na
EX4-risk	14	16	21	12	na	9	na
EX5-10	17	21	27	6	na	6	na
EX5-20	17	25	26	7	na	6	na
EX5-40	18	22	30	7	na	5	na
EX5-80	23	24	31	8	na	5	na
EX6-10	11	16	26	13	na	10	na
EX6-20	11	15	35	15	na	10	na
EX6-40	11	26	50	13	na	12	na
EX6-60	14	26	62	14	na	11	na

Table 3: Comparison between full system, normal equations, and other methods

	Alg.4.4(full)	ppc	inexact_pc
EX1-50	13	16	13
EX1-75	16	19	13
EX1-100	15	19	14
EX1-200	14	21	18
EX2-50	9	13	12
EX2-100	8	11	8
EX2-150	9	15	8
EX2-200	10	11	10
EX3-10-4	13	15	13
EX3-20-4	11	17	15
EX3-30-9	11	17	11
EX3-40-9	13	19	13
EX4-mark	12	15	13
EX4-return	15	17	13
EX4-risk	14	19	13
EX5-10	17	20	18
EX5-20	17	27	29
EX5-40	18	f	29
EX5-80	23	43	29
EX6-10	11	20	11
EX6-20	11	11	11
EX6-40	11	17	12
EX6-60	14	17	13

We also show the results for using the full system and the normal equations. In the tables, 'f' denotes failure. SDPT3 and LOQO do not handle rotated cone constraints. Our best method performs quite well compared to the other codes. As the evaluation [7] had shown, the code MOSEK which is the only one specialized for convex optimization including SOCP is the most robust and efficient for such problems. Its performance is very comparable to that of our best method because the approaches are very similar except for a better exploitation of sparsity in MOSEK. SeDuMi uses also a self-dual embedding technique and was mainly optimized for robustness, which is reflected in the uniformly moderate but not lowest iteration counts and the lack of failures. SDPT3 uses an infeasible path-following method and could probably handle larger sparse cases nearly as well as MOSEK. LOQO finally, is a general NLP code and it treats the SOCP problems as smoothed nondifferentiable NLPs which in some cases leads to larger iteration counts.