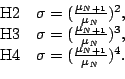Next: Predictor-Corrector Algorithms
Up: Numerical realization and results
Previous: Linear system
In this section, we start by stating the long-step path-following
algorithm with the scaled search direction and then compare the
heuristic choices of the centering parameter 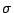 with the
proposed choices. First, we give the linear system for the scaled
search direction,
with the
proposed choices. First, we give the linear system for the scaled
search direction,
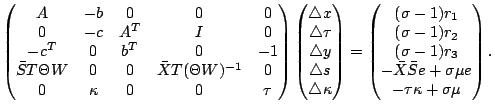 |
(4-3) |
In algorithms, we denote
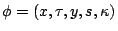 and all other
5-tuple vectors are also converted to
and all other
5-tuple vectors are also converted to
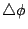 ,
,
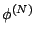 , and etc.
, and etc.
In the basic algorithm, the parameter
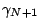 is fixed for
all iterations. Here, we consider that
is fixed for
all iterations. Here, we consider that 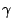 can be changed at
each iteration and propose a way to choose
can be changed at
each iteration and propose a way to choose
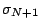 and
and
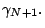 We also compare this choice with the heuristic
choices of
We also compare this choice with the heuristic
choices of
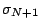 and fixed
and fixed 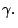 Since the
comparisons are based on the same algorithm, we only compare the
number of iterations.
Since the
comparisons are based on the same algorithm, we only compare the
number of iterations.
Let us consider three heuristic choices with fixed
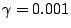 :
:
We now present the algorithm for choosing 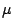 and
and 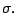
In the literature, authors seldom show exactly how 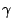 and
and
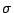 are chosen. Although these heuristic choices of
are chosen. Although these heuristic choices of 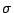 are mentioned frequently in the literature, practical algorithms
must develop more robust methods to choose
are mentioned frequently in the literature, practical algorithms
must develop more robust methods to choose 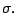 As one can
see in Table 1, the performances of H2, H3, and H4
vary in each problem. The main idea of Algorithm4.3 is to
use three heuristic choices and to change the size of the
neighborhood according to the result of H2. If
As one can
see in Table 1, the performances of H2, H3, and H4
vary in each problem. The main idea of Algorithm4.3 is to
use three heuristic choices and to change the size of the
neighborhood according to the result of H2. If 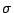 is greater
than
is greater
than
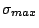 , it follows that the descent of
, it follows that the descent of 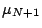 is small. One way to achieve larger descent is to have a larger
neighborhood, i.e., choosing a smaller
is small. One way to achieve larger descent is to have a larger
neighborhood, i.e., choosing a smaller 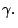 If
If 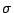 is
less than
is
less than
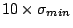 , it means that a large descent
has been made. When
, it means that a large descent
has been made. When 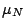 is getting closer to the tolerance, it
is important to pull the new point back to the central path, i.e.,
choosing larger
is getting closer to the tolerance, it
is important to pull the new point back to the central path, i.e.,
choosing larger 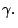 If
If 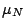 is still large, we use H4 to
loosen the centering parameter. The reason is that the small value
of H2 indicates that the current neighborhood is large enough to
allow for a large descent. The following table shows the number
of iterations for reaching the optimum using Algorithm
4.2 combined with the above four methods to choose
is still large, we use H4 to
loosen the centering parameter. The reason is that the small value
of H2 indicates that the current neighborhood is large enough to
allow for a large descent. The following table shows the number
of iterations for reaching the optimum using Algorithm
4.2 combined with the above four methods to choose
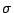 and
and 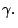
Table 1:
The number of iterations for different methods of choosing 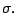
|
Algorithm 4.3 |
H2 |
H3 |
H4 |
| EX1-50 |
20 |
25 |
23 |
24 |
| EX1-75 |
21 |
27 |
25 |
25 |
| EX1-100 |
22 |
28 |
25 |
26 |
| EX1-200 |
23 |
28 |
28 |
28 |
| EX2-50 |
13 |
18 |
18 |
21 |
| EX2-100 |
13 |
19 |
18 |
21 |
| EX2-150 |
14 |
19 |
20 |
21 |
| EX2-200 |
14 |
18 |
18 |
18 |
| EX3-10-4 |
18 |
24 |
25 |
25 |
| EX3-20-4 |
16 |
21 |
22 |
23 |
| EX3-30-9 |
18 |
23 |
24 |
25 |
| EX3-40-9 |
18 |
24 |
23 |
26 |
| EX4-mark |
18 |
27 |
25 |
27 |
| EX4-return |
23 |
30 |
30 |
29 |
| EX4-risk |
21 |
27 |
26 |
29 |
| EX5-10 |
27 |
30 |
33 |
31 |
| EX5-20 |
26 |
32 |
31 |
33 |
| EX5-40 |
30 |
35 |
37 |
36 |
| EX5-80 |
31 |
36 |
35 |
38 |
| EX6-10 |
26 |
28 |
34 |
33 |
| EX6-20 |
35 |
36 |
42 |
43 |
| EX6-40 |
50 |
57 |
57 |
58 |
| EX6-60 |
62 |
66 |
71 |
79 |
| Total |
559 |
678 |
690 |
721 |
According to this table, we see that the number of iterations
using Algorithm 4.3 is overall less than using the heuristic
choices. The average is about 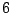 iterations less than H2, and H3,
iterations less than H2, and H3,
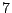 iterations less than H4. Since the problem is large, the
running time for 6 or 7 iterations is still significant. Figure
1 from EX6-40 shows that
iterations less than H4. Since the problem is large, the
running time for 6 or 7 iterations is still significant. Figure
1 from EX6-40 shows that 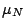 decreases much more
in Algorithm 4.3 than in the other three methods. Similar
graphs can be obtained for each test case.
decreases much more
in Algorithm 4.3 than in the other three methods. Similar
graphs can be obtained for each test case.



Next: Predictor-Corrector Algorithms
Up: Numerical realization and results
Previous: Linear system
Hans D. Mittelmann
2003-09-10
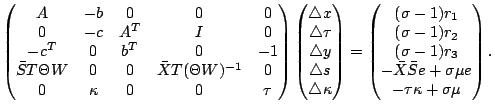
![]() is fixed for
all iterations. Here, we consider that
is fixed for
all iterations. Here, we consider that ![]() can be changed at
each iteration and propose a way to choose
can be changed at
each iteration and propose a way to choose
![]() and
and
![]() We also compare this choice with the heuristic
choices of
We also compare this choice with the heuristic
choices of
![]() and fixed
and fixed ![]() Since the
comparisons are based on the same algorithm, we only compare the
number of iterations.
Since the
comparisons are based on the same algorithm, we only compare the
number of iterations.
![]() :
: