


Next: Bibliography
Up: Interior Point Methods for
Previous: Predictor-Corrector Algorithms
Throughout this study, we discuss second-order
cone programming theoretically as well as practically. Both the
long-step path-following and predictor-corrector algorithms are
studied. Existence of the step length 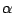 is shown for the
long-step method. Furthermore, a specific algorithm for choosing
the centering parameter
is shown for the
long-step method. Furthermore, a specific algorithm for choosing
the centering parameter 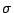 and the size of the neighborhood
and the size of the neighborhood
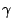 is developed and tested successfully on our test cases.
Next, several variants of predictor-corrector algorithms are also
compared. We analyze the numerical behavior of the linear and
quadratic combinations of predictor and corrector directions. The
idea of inexact Newton's method and of repeating the predictor
direction one more time are also integrated into the algorithm.
According to our numerical results, the inexact method for SOCP
can be expected to behave similarly as in LP. Overall, Algorithm
4.4 using the normal equations works best for both full and sparse
cases. The linear constraints in Example 5 lead to a full matrix.
The inexact method works competitively in every case except
Example 5.
is developed and tested successfully on our test cases.
Next, several variants of predictor-corrector algorithms are also
compared. We analyze the numerical behavior of the linear and
quadratic combinations of predictor and corrector directions. The
idea of inexact Newton's method and of repeating the predictor
direction one more time are also integrated into the algorithm.
According to our numerical results, the inexact method for SOCP
can be expected to behave similarly as in LP. Overall, Algorithm
4.4 using the normal equations works best for both full and sparse
cases. The linear constraints in Example 5 lead to a full matrix.
The inexact method works competitively in every case except
Example 5.
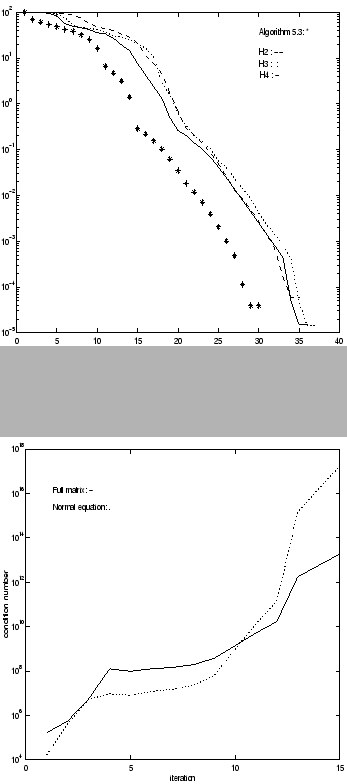
Figure 2:
The condition number of the coefficient matrix for full linear system and normal equations
Figure 1:
Comparison of 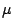 from Algorithm 4.3, H2,H3,H4
from Algorithm 4.3, H2,H3,H4
 |



Next: Bibliography
Up: Interior Point Methods for
Previous: Predictor-Corrector Algorithms
Hans D. Mittelmann
2003-09-10

