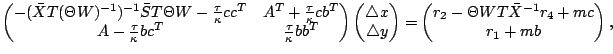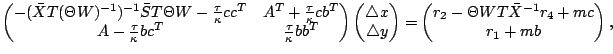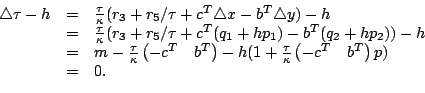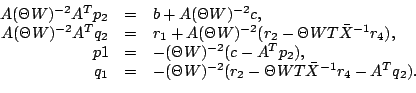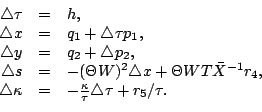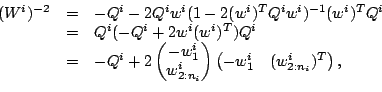Next: Long-step path-following method
Up: Numerical realization and results
Previous: Numerical realization and results
Here, we will discuss some computational issues in second order
cone programming, especially the linear system
(1-6). Denote by
![$ [r_1,r_2,r_3,r_4,r_5]^T$](img325.gif) the right
hand side of (1-6). The augmented system following
from (1-6) is
where
the right
hand side of (1-6). The augmented system following
from (1-6) is
where
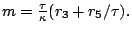 We use the NT
direction, i.e.,
We use the NT
direction, i.e.,
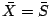 , apply the
Sherman-Morrison-Woodury formula to the coefficient matrix, and
denote
, apply the
Sherman-Morrison-Woodury formula to the coefficient matrix, and
denote
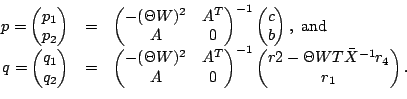 |
(4-1) |
Hence,
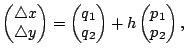 where where 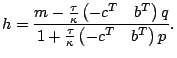 |
(4-2) |
The next lemma follows immediately.
Moreover, the normal equations are
Subsequently,
the search direction can be computed as follows:
Furthermore, one can rewrite
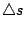 as
Two vectors
as
Two vectors
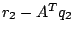 and
and 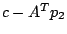 have been calculated
while computing
have been calculated
while computing 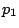 and
and 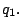 Because of the definition of
Because of the definition of
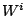 ,
, 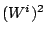 and
and
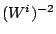 are easy to obtain:
since
are easy to obtain:
since
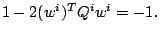



Next: Long-step path-following method
Up: Numerical realization and results
Previous: Numerical realization and results
Hans D. Mittelmann
2003-09-10