

Next: Discretization of the distributed
Up: Discretization and optimization techniques
Previous: Discretization and optimization techniques
Let 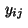 denote approximations of the state variables
denote approximations of the state variables
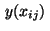 for
for
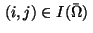 and let
and let 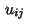 be approximations for
the control variables
be approximations for
the control variables 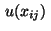 for
for
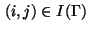 .
We specify the functions
.
We specify the functions
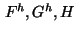 for the optimization
problem (1) corresponding to problem
(1)-(6) as follows.
The optimization variable
for the optimization
problem (1) corresponding to problem
(1)-(6) as follows.
The optimization variable 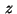 in (1) is taken as the vector
in (1) is taken as the vector
Note that we do not consider the variables
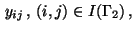 explicitly as optimization variables since they
are prescribed by the Dirichlet condition (4).
explicitly as optimization variables since they
are prescribed by the Dirichlet condition (4).
Equality constraints
are obtained by applying the five-point-star to the
elliptic equation
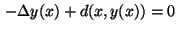 in (2) in all points
in (2) in all points 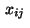 with
with
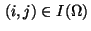 ,
,
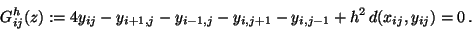 |
(3) |
In these equations may appear the undefined variables
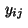 for
for
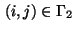 .
These variables have to be substituted by the
Dirichlet conditions (4),
.
These variables have to be substituted by the
Dirichlet conditions (4),
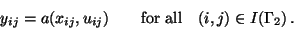 |
(4) |
The derivative
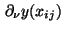 in the direction of
the outward normal is approximated by the expression
in the direction of
the outward normal is approximated by the expression
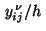 where
where
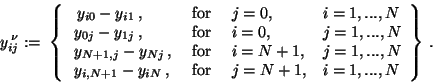 |
(5) |
Then the discrete form of the Neumann boundary condition (3)
leads to the equality constraints
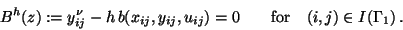 |
(6) |
The control and state inequality constraints (5) and
(6) yield the inequality constraints
| |
|
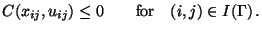 |
(7) |
| |
|
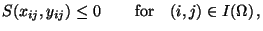 |
(8) |
Observe that the inequality constraints do not depend on the meshsize
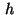 . Later on, this fact will require a scaling of the Lagrange
multipliers.
Finally, the discretized form of the cost function (1) is
. Later on, this fact will require a scaling of the Lagrange
multipliers.
Finally, the discretized form of the cost function (1) is
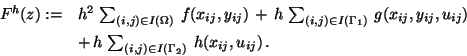 |
(9) |
Then the relations (2)-(8)
define an NLP-problem of the form (1).
Associate Lagrange multipliers
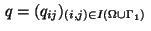 ,
,
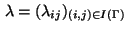 and
and
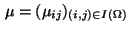 with the equality constraints
(3) and (6)
resp. the inequality constraints (7) and (8).
Then the Lagrangian function for the above NLP-problem becomes:
with the equality constraints
(3) and (6)
resp. the inequality constraints (7) and (8).
Then the Lagrangian function for the above NLP-problem becomes:
The multipliers 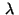 and
and 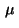 satisfy complementarity
conditions corresponding to (14):
satisfy complementarity
conditions corresponding to (14):
Now we discuss the necessary conditions of optimality
for state and control variables assuming
different combinations of indices 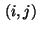 .
For state variables with indices
.
For state variables with indices
 we obtain the relations
we obtain the relations
These equations contain multipliers 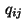 for
for
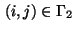 that do not appear in the Lagrangian (10). To make
equations and definitions consistent, we put
that do not appear in the Lagrangian (10). To make
equations and definitions consistent, we put
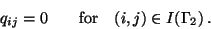 |
(12) |
This substitution corresponds to the Dirichlet condition (11).
Relations (11) then reveal that the Lagrange multipliers
 satisfy the five-point-star difference equations for the adjoint equation
satisfy the five-point-star difference equations for the adjoint equation
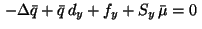 in (9)
if we use the following approximation for the Borel measure
in (9)
if we use the following approximation for the Borel measure 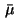 ,
,
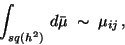 |
(13) |
where 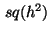 denotes a square centered at
denotes a square centered at 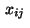 with area
with area 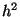 .
Recall the decomposition (15) of the measure
.
Recall the decomposition (15) of the measure
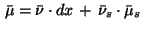 .
If the singular part of the measure vanishes,
i.e.
.
If the singular part of the measure vanishes,
i.e.
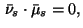 then (13) yields the following appro-
then (13) yields the following appro-
ximation for the density 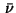 ,
,
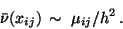 |
(14) |
In case that the measure
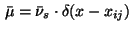 is a delta distribution,
we obtain from (13) the relation
is a delta distribution,
we obtain from (13) the relation
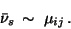 |
(15) |
On the boundary part 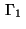 we get for indices
we get for indices
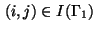 assuming, e.g.,
assuming, e.g.,
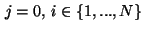 :
:
Recalling (5) this represents the discrete version of the Neumann boundary condition (10).
Finally, necessary conditions with respect to the control variables
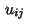 for indices
for indices
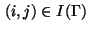 are determined by the
following two relations.
For
are determined by the
following two relations.
For
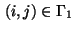 with, e.g.,
with, e.g.,
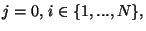 we get
we get
This equation yields the discrete version of the optimality condition
(12) for the control, if we use the identification
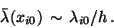 |
(16) |
For indices
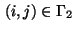 with, e.g.,
with, e.g.,
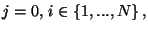 we find
we find
Observing 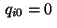 and
the approximation (5) of the normal derivative,
the minimum condition (13) holds with the substitutions
and
the approximation (5) of the normal derivative,
the minimum condition (13) holds with the substitutions
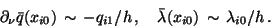 |
(17) |

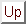

Next: Discretization of the distributed
Up: Discretization and optimization techniques
Previous: Discretization and optimization techniques
Hans D. Mittelmann
2000-12-09
![]() in (2) in all points
in (2) in all points ![]() with
with
![]() ,
,
![]() ,
,
![]() and
and
![]() with the equality constraints
(3) and (6)
resp. the inequality constraints (7) and (8).
Then the Lagrangian function for the above NLP-problem becomes:
with the equality constraints
(3) and (6)
resp. the inequality constraints (7) and (8).
Then the Lagrangian function for the above NLP-problem becomes:
![]() we get for indices
we get for indices
![]() assuming, e.g.,
assuming, e.g.,
![]() :
:
![\begin{eqnarray*}
0= L_{y_{i0}} =
&& -q_{i1} + q_{i0} -q_{i0}\,h\,b_y(x_{i0},y_...
...,- q_{i0}\,b_y(x_{i0},y_{i0}) +
g_y(x_{i0},y_{i0},u_{i0})\,] \,.
\end{eqnarray*}](img177.gif)
![]() for indices
for indices
![]() are determined by the
following two relations.
For
are determined by the
following two relations.
For
![]() with, e.g.,
with, e.g.,
![]() we get
we get
![\begin{eqnarray*}
0= L_{u_{i0}} && = h\,g_u(x_{i0},y_{i0},u_{i0}) -
q_{i0}\,h\,...
...i0},u_{i0}) +
\frac{\lambda_{i0}}{h}\,C_u(x_{i0},u_{i0})\,] \,.
\end{eqnarray*}](img180.gif)
![\begin{eqnarray*}
0= L_{u_{i0}}
&&
= h\,k_u(x_{i0},u_{i0}) - q_{i1}\,a_u(x_{i0}...
...x_{i0},u_{i0}) +
\frac{\lambda_{i0}}{h}\,C_u(x_{i0},u_{i0})\,]
\end{eqnarray*}](img183.gif)