

Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Discretization of the boundary
The optimization variable 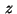 in (1) is now taken as the vector
in (1) is now taken as the vector
Due to the Dirichlet conditions (28), the variables
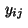 for
for
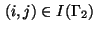 can be eliminated from the optimization process.
can be eliminated from the optimization process.
The application of the five-point-star to the
elliptic equation
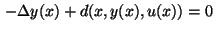 in (26) yields the following equations for all
in (26) yields the following equations for all
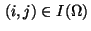 :
:
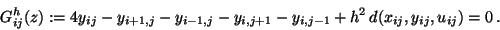 |
(18) |
The Dirichlet condition (28) is incorporated by fixing the values
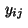 on
on 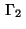 :
:
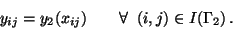 |
(19) |
Observing the approximation (5) of the outward normal derivative,
the discrete form of the Neumann boundary condition in (27)
leads to the equality constraints
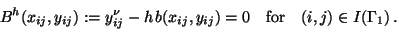 |
(20) |
The control and state inequality constraints (29) and
(30) yield the inequality constraints
| |
|
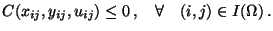 |
(21) |
| |
|
 |
(22) |
Note again that these inequality constraints do not depend on the
meshsize 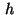 .
The discretized form of the cost function (25) is
.
The discretized form of the cost function (25) is
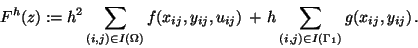 |
(23) |
Hence, for distributed control problems the NLP-problem (1)
is given by the relations (18)-(23).
The corresponding Lagrangian function is
where the Lagrange multipliers
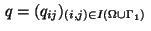 ,
,
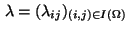 and
and
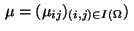 are associated with
the equality constraints (18) and (20),
resp. the inequality constraints (21) and (22).
The multipliers
are associated with
the equality constraints (18) and (20),
resp. the inequality constraints (21) and (22).
The multipliers 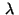 and
and 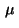 satisfy complementarity
conditions corresponding to (37):
satisfy complementarity
conditions corresponding to (37):
The discussion of the necessary conditions of optimality
is similar to that for boundary control problems.
For state variables 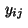 with indices
with indices
 we obtain the relations
we obtain the relations
Here as in (12), the undefined multipliers are set to
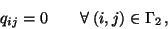 |
(26) |
in accordance with the Dirichlet condition (35).
We deduce from equations (25) that the Lagrange multipliers
 satisfy the five-point-star difference equations for the adjoint equation
satisfy the five-point-star difference equations for the adjoint equation
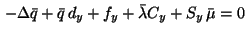 in (33)
if we approximate the measure
in (33)
if we approximate the measure  and the multiplier function
and the multiplier function
 in
in 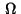 by
by
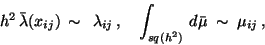 |
(27) |
where 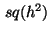 denotes a square centered at
denotes a square centered at  with area
with area 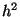 .
Recall again the decomposition (38) of the measure
.
Recall again the decomposition (38) of the measure
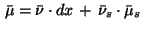 .
If the singular part of the measure vanishes,
then (27) yields an approximation for the density
.
If the singular part of the measure vanishes,
then (27) yields an approximation for the density 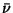 ,
,
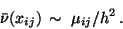 |
(28) |
while for a delta distribution
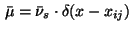 we deduce from (27) the approximation
we deduce from (27) the approximation
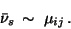 |
(29) |
For indices
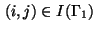 on the boundary
on the boundary 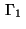 we obtain, e.g., for
we obtain, e.g., for
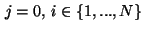 ,
,
which constitutes the discrete version of the Neumann boundary condition
(34).
Finally, necessary conditions with respect to the control variables
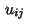 for
for
 are determined by
are determined by
>From this equation we can recover the discrete version of the control law
(12), if we use the identification
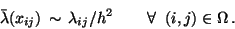 |
(30) |


Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Discretization of the boundary
Hans D. Mittelmann
2000-12-09
![]() on the boundary
on the boundary ![]() we obtain, e.g., for
we obtain, e.g., for
![]() ,
,
![]() for
for
![]() are determined by
are determined by