

Next: Discretization of the boundary
Up: paper87
Previous: Distributed Control Problem
Discretization and optimization techniques
The discussion of discretization schemes is restricted to the standard
situation where
the domain is the unit square
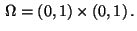 The purpose of this section is to develop discretization techniques by
which the boundary control
problem (1)-(6) and the
distributed control problem (25)-(30)
are transformed into a nonlinear programming problem (NLP-problem) of the form
The purpose of this section is to develop discretization techniques by
which the boundary control
problem (1)-(6) and the
distributed control problem (25)-(30)
are transformed into a nonlinear programming problem (NLP-problem) of the form
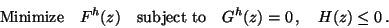 |
(1) |
The functions 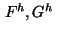 and
and 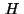 are sufficiently smooth and are of
appropriate dimension.
The upper subscript
are sufficiently smooth and are of
appropriate dimension.
The upper subscript 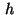 denotes the dependence on the stepsize.
The optimization variable
denotes the dependence on the stepsize.
The optimization variable 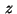 will comprise both the
discretized state and control variables.
will comprise both the
discretized state and control variables.
The form (1) will be achieved by solving
the elliptic equation (2) resp. (26)
with the standard five-point-star discretization scheme.
Choose a number
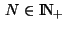 and the stepsize
and the stepsize
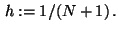 Consider the mesh points
Consider the mesh points
and define the following sets of indices 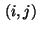 residing either in the domain
residing either in the domain 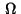 or on the four edges of
the boundary
or on the four edges of
the boundary 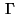 :
:
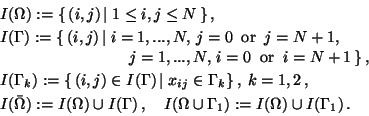 |
(2) |
Obviously, we have
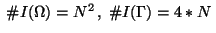 ;
define further
;
define further
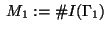 .
.
We shall first discuss discretization schemes for the boundary control
problem and will then only indicate the necessary
modifications to obtain schemes for the distributed control problem.
Subsections


Next: Discretization of the boundary
Up: paper87
Previous: Distributed Control Problem
Hans D. Mittelmann
2000-12-09
![]() and the stepsize
and the stepsize
![]() Consider the mesh points
Consider the mesh points