

Next: A distributed control example
Up: Numerical examples
Previous: Numerical examples
In this section an example from heat conduction is chosen to demonstrate
the viability of the proposed approach. It is meant to be typical for
practical problems that have to be solved in industrial and other applications.
A mathematical description of the problem is as follows. The underlying boundary
value problem is Laplace's equation on the unit square, corresponding to no
internal heat sources, coupled with mixed boundary conditions, namely
homogeneous Neumann conditions on 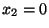 , or no heat flux across this boundary,
a heat flux proportional to the temperature at the boundaries
, or no heat flux across this boundary,
a heat flux proportional to the temperature at the boundaries 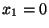 and
and
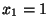 , while the solution is controlled on
, while the solution is controlled on 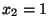 . The control function
is to be found such that the temperature in the central subsquare of length
. The control function
is to be found such that the temperature in the central subsquare of length
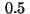 is as close as possible to a given function
is as close as possible to a given function 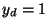 in the
in the
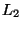 -norm.
In the first version of the problem a multiple
-norm.
In the first version of the problem a multiple 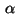 of a
regularizing boundary
integral over the control function is added to the objective functional,
while without this a bang-bang control may be expected in the second version.
To complete the problem definition upper and lower bounds of
of a
regularizing boundary
integral over the control function is added to the objective functional,
while without this a bang-bang control may be expected in the second version.
To complete the problem definition upper and lower bounds of 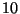 respectively
respectively
 are imposed on both state and control.
are imposed on both state and control.
Thus letting
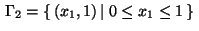 and
and
![$\,\Omega_0= [0.25,0.75]^2 \,$](img226.gif) ,
the control problem is to determine a function
,
the control problem is to determine a function
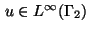 which minimizes
which minimizes
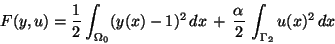 |
(1) |
subject to the state equation, Neumann and Dirichlet boundary conditions
and control and state inequality constraints,
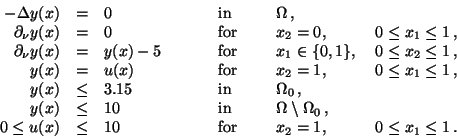 |
(2) |
The NLP-problem to be solved is given by (3)-(9).
It is a linearly constrained convex quadratic program.
Case
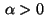 :
The following table lists the results for four different optimization packages
with an AMPL interface and one, BPMPD, which was applied after translating
the AMPL file into extended MPS format. For a reference to AMPL, the codes, and
the MPS format as well as for other benchmarks, see [31].
An asterisk denotes failure, while
otherwise the CPU seconds on a Linux-PC with 450MHz PII and 512 MB are listed.
The optimization problem of the largest instance has
:
The following table lists the results for four different optimization packages
with an AMPL interface and one, BPMPD, which was applied after translating
the AMPL file into extended MPS format. For a reference to AMPL, the codes, and
the MPS format as well as for other benchmarks, see [31].
An asterisk denotes failure, while
otherwise the CPU seconds on a Linux-PC with 450MHz PII and 512 MB are listed.
The optimization problem of the largest instance has 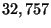 variables
and
variables
and 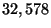 constraints. A probable reason for the failures of SNOPT and
MINOS is the near linear independence of the equality constraints which
causes an increasing ill-conditioning with growing N.
constraints. A probable reason for the failures of SNOPT and
MINOS is the near linear independence of the equality constraints which
causes an increasing ill-conditioning with growing N.
Table 1:
Results for Example 4.1,
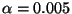
| N |
LOQO |
SNOPT |
LANC |
MINOS |
BPMPD |
 |
| 60 |
13 |
41 |
1126 |
18 |
4 |
.2789728 |
| 120 |
203 |
* |
29561 |
369 |
* |
.2590819 |
| 180 |
722 |
* |
* |
* |
186 |
.2530543 |
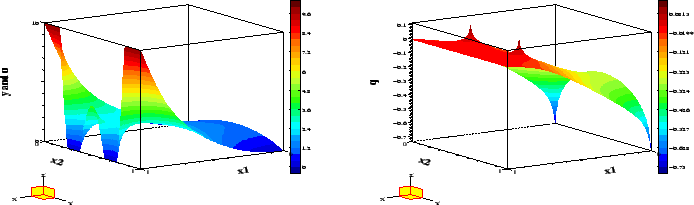
Figure 1:
Example 4.1,
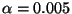 :
Optimal control on
:
Optimal control on  and adjoint variable
and adjoint variable  .
.
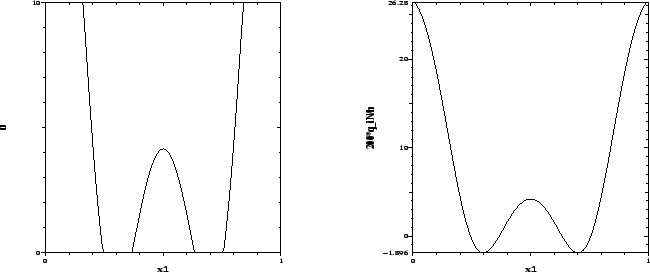 |
Figure 2:
Example 4.1,
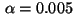 :
Optimal state and adjoint variable on
:
Optimal state and adjoint variable on  .
.
 |
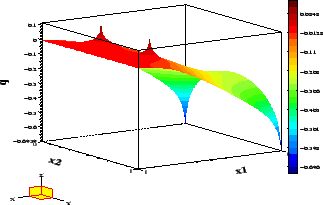
The optimal control and adjoint variable for the weight
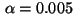 are shown in Figure 1. It is instructive to discuss the necessary conditions (19)-(23)
that apply in this case. The state constraint
are shown in Figure 1. It is instructive to discuss the necessary conditions (19)-(23)
that apply in this case. The state constraint
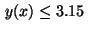 for
for
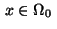 becomes active at two points
becomes active at two points
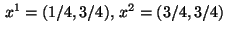 , while the state constraint
, while the state constraint
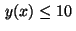 in
in
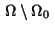 does not become active.
Hence, the adjoint equations (19) are
does not become active.
Hence, the adjoint equations (19) are
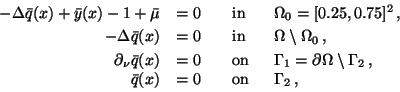 |
(3) |
where the measure is given by
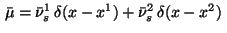 .
The approximation (15) yields the values
.
The approximation (15) yields the values
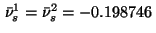 .
The optimal state and adjoint variable on
.
The optimal state and adjoint variable on 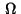 are displayed
in Figure 2.
are displayed
in Figure 2.
The minimum condition reduces to the case (22)
with
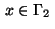 since no control is applied on the
Neumann boundary
since no control is applied on the
Neumann boundary 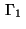 . In view of
. In view of
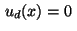 we get from
(22) for all
we get from
(22) for all
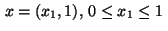 :
:
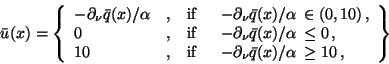 |
(4) |
In order to evaluate its discrete analogon, we recall definition
(5) and relation (17) which give
Hence, the discrete version of the minimum condition (4)
requires to check the conditions
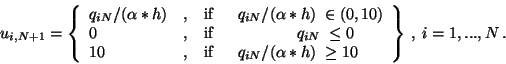 |
(5) |
By inspecting Figure 1, the reader may verify this condition for the
value
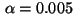 .
.
Case
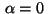 :
Table 2 lists the results for the five optimization packages
used in Table 1.
:
Table 2 lists the results for the five optimization packages
used in Table 1.
Table 2:
Results for Example 4.1, 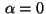
| N |
LOQO |
SNOPT |
LANC |
MINOS |
BPMPD |
 |
| 60 |
15 |
149 |
1516 |
17 |
5 |
.1771073 |
| 120 |
220 |
* |
25868 |
398 |
57 |
.1574154 |
| 180 |
939 |
* |
* |
* |
243 |
.1512835 |
Figure 3:
Example 4.1, 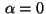 : Optimal state and control.
: Optimal state and control.
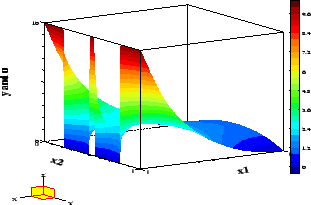 |
Figure 4:
Example 4.1, 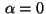 : Optimal control on
: Optimal control on  and switching function
and switching function 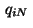 .
.
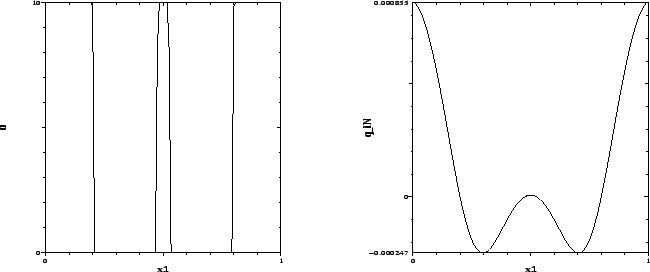 |
Figure 5:
Example 4.1,  : Adjoint variable on
: Adjoint variable on  .
.
 |
The adjoint equation agrees with equation (3).
The optimal control shown in Figure 4 is bang-bang. Accordingly, the
minimum condition (24) yields the control law
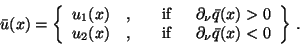 |
(6) |
Its discrete variant yields in analogy to (5),
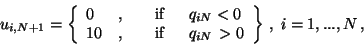 |
(7) |
which is confirmed by Figure 4.


Next: A distributed control example
Up: Numerical examples
Previous: Numerical examples
Hans D. Mittelmann
2000-12-09
![]() and
and
![]() ,
the control problem is to determine a function
,
the control problem is to determine a function
![]() which minimizes
which minimizes
![]() :
The following table lists the results for four different optimization packages
with an AMPL interface and one, BPMPD, which was applied after translating
the AMPL file into extended MPS format. For a reference to AMPL, the codes, and
the MPS format as well as for other benchmarks, see [31].
An asterisk denotes failure, while
otherwise the CPU seconds on a Linux-PC with 450MHz PII and 512 MB are listed.
The optimization problem of the largest instance has
:
The following table lists the results for four different optimization packages
with an AMPL interface and one, BPMPD, which was applied after translating
the AMPL file into extended MPS format. For a reference to AMPL, the codes, and
the MPS format as well as for other benchmarks, see [31].
An asterisk denotes failure, while
otherwise the CPU seconds on a Linux-PC with 450MHz PII and 512 MB are listed.
The optimization problem of the largest instance has ![]() variables
and
variables
and ![]() constraints. A probable reason for the failures of SNOPT and
MINOS is the near linear independence of the equality constraints which
causes an increasing ill-conditioning with growing N.
constraints. A probable reason for the failures of SNOPT and
MINOS is the near linear independence of the equality constraints which
causes an increasing ill-conditioning with growing N.
![]() are shown in Figure 1. It is instructive to discuss the necessary conditions (19)-(23)
that apply in this case. The state constraint
are shown in Figure 1. It is instructive to discuss the necessary conditions (19)-(23)
that apply in this case. The state constraint
![]() for
for
![]() becomes active at two points
becomes active at two points
![]() , while the state constraint
, while the state constraint
![]() in
in
![]() does not become active.
Hence, the adjoint equations (19) are
does not become active.
Hence, the adjoint equations (19) are
![]() since no control is applied on the
Neumann boundary
since no control is applied on the
Neumann boundary ![]() . In view of
. In view of
![]() we get from
(22) for all
we get from
(22) for all
![]() :
:
![]() :
Table 2 lists the results for the five optimization packages
used in Table 1.
:
Table 2 lists the results for the five optimization packages
used in Table 1.