

Next: Bibliography
Up: Numerical examples
Previous: A boundary control example
In this section we consider an optimal control problem for a semilinear elliptic equation of logistic type which was studied in Leung, Stojanovic
[25,34]. The problem is to determine a distributed control
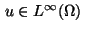 that minimizes the functional
that minimizes the functional
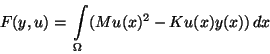 |
(8) |
subject to the elliptic state equation
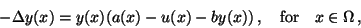 |
(9) |
homogeneous Neumann boundary conditions,
 |
|
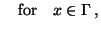 |
(10) |
and
control and state inequality constraints
| |
|
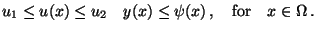 |
(11) |
Here, 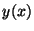 denotes
the population of a biological species,
denotes
the population of a biological species, 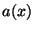 a spatially dependent
intrinsic growth rate,
a spatially dependent
intrinsic growth rate, 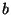 the crowding effect, while
the crowding effect, while 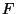 denotes the
difference between economic cost and revenue,
with nonnegative constants
denotes the
difference between economic cost and revenue,
with nonnegative constants 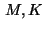 .
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [12]. Three numerical methods, two of
interior point type, were compared in [2] for linear
problems and homogeneous Dirichlet conditions.
.
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [12]. Three numerical methods, two of
interior point type, were compared in [2] for linear
problems and homogeneous Dirichlet conditions.
The adjoint equations (33), (34) applied to problem
(8)-(11) lead to
The minimum condition (40) gives the following two control laws.
For
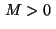 we get
we get
![\begin{displaymath}
\bar{u}(x) = P_{[u_1,u_2]}
\left ( \frac{1}{2M}\,[\,(K - \bar{q}(x))\,\bar{y}(x)\,] \right ) \,,
\end{displaymath}](img265.gif) |
(12) |
where
![$\,P_{[u_1,u_2]}\,$](img266.gif) denotes the projection operator on the interval
denotes the projection operator on the interval
![$\,[u_1,u_2]\,$](img267.gif) .
In case
.
In case 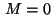 we can put
we can put 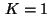 and obtain
and obtain
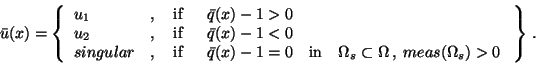 |
(13) |
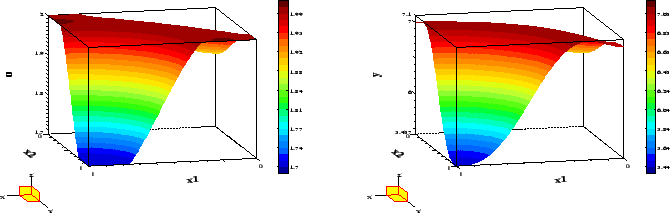
Figure 6:
Optimal control and state for Example 4.2, 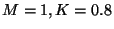 .
.
 |
For the sake of reference the data were chosen as in [25], Example 5.2:
For this case the computational approach of [25] is not valid.
Additionally, bound and state constraints were chosen: 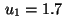 ,
,
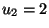 ,
, 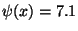 . Both types of bounds become active.
The optimal control and state are shown in Figure 6. The reader may verify
that the control law (12) is satisfied.
The state variable attains its upper bound at the two
points
. Both types of bounds become active.
The optimal control and state are shown in Figure 6. The reader may verify
that the control law (12) is satisfied.
The state variable attains its upper bound at the two
points
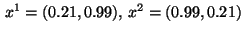 near the boundary.
It has to be noted that this example leads to a difficult nonlinear
optimization problem which is not a QP anymore but a quadratically constrained
quadratic program. Thus, the QP solver BPMPD is not applicable.
For testing the local optimality of the computed solution, second-order
sufficient conditions would need to be evaluated. To the best of our
knowledge for this class of elliptic problems the literature does not
provide a verifiable set of such conditions. A practical test could be
devised by checking the positive definiteness of the projected Hessian of
the Lagrangian. This test will be part of our future work.
near the boundary.
It has to be noted that this example leads to a difficult nonlinear
optimization problem which is not a QP anymore but a quadratically constrained
quadratic program. Thus, the QP solver BPMPD is not applicable.
For testing the local optimality of the computed solution, second-order
sufficient conditions would need to be evaluated. To the best of our
knowledge for this class of elliptic problems the literature does not
provide a verifiable set of such conditions. A practical test could be
devised by checking the positive definiteness of the projected Hessian of
the Lagrangian. This test will be part of our future work.
In the following tables an asterisk denotes failure and an "m" that the
available memory was exceeded.
The fact that made the previous problem and those in
[28,29] difficult for SQP-based methods, namely the near linear
dependence of the constraints, here the discretized boundary value problem,
which exhibits increasing ill-conditioning for growing 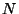 , is even more
pronounced through the homogeneous Neumann conditions resulting in singular
constraints.
The largest instance has
, is even more
pronounced through the homogeneous Neumann conditions resulting in singular
constraints.
The largest instance has 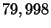 variables and
variables and 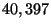 constraints in the
NLP problem. These results were obtained on a HP9000-K260 with 256MB.
constraints in the
NLP problem. These results were obtained on a HP9000-K260 with 256MB.
Table 3:
Results for Example 4.2, 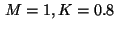 .
.
| N |
LOQO |
SNOPT |
LANC |
MINOS |
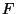 |
| 50 |
218 |
3281 |
2356 |
289 |
-6.485781 |
| 100 |
2141 |
m |
103794 |
5331 |
-6.576428 |
| 200 |
28517 |
m |
* |
* |
-6.620092 |
Table 4:
Results for Example 4.2, 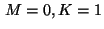 .
.
| N |
LOQO |
SNOPT |
LANC |
MINOS |
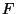 |
| 50 |
77 |
7384 |
3704 |
267 |
-18.48254 |
| 100 |
3012 |
m |
116328 |
* |
-18.73615 |
| 200 |
57264 |
m |
* |
* |
-18.86331 |
To confirm that a bang-bang control can occur in this problem the case
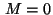 ,
, 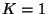 ,
, 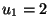 ,
, 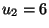 ,
, 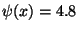 was solved.
The optimal control and state are shown in Figure 7.
Both the control and the state constraints become active.
The adjoint variable and the switching curves
was solved.
The optimal control and state are shown in Figure 7.
Both the control and the state constraints become active.
The adjoint variable and the switching curves 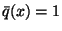 displayed in Figure 8 admit a verification of the
control law (13).
While the CPU times for
displayed in Figure 8 admit a verification of the
control law (13).
While the CPU times for 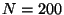 are excessive, the accuracy for
are excessive, the accuracy for 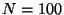 should be sufficient and the times are acceptable. To avoid the trivial
solution
should be sufficient and the times are acceptable. To avoid the trivial
solution 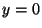 of the state equation nonzero starting values for the
state were chosen in this example. As in the case
of the state equation nonzero starting values for the
state were chosen in this example. As in the case 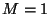 , the local
optimality of the solution shown in Figure 7 would need to be verified.
, the local
optimality of the solution shown in Figure 7 would need to be verified.
Figure 7:
Optimal control and state for Example 4.2, 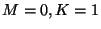 .
.
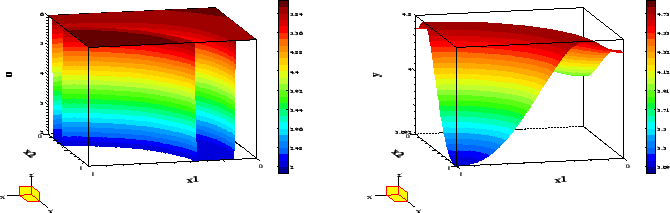 |
Figure 8:
Optimal adjoint variable and switching curves for Example 4.2, 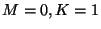 .
.
 |


Next: Bibliography
Up: Numerical examples
Previous: A boundary control example
Hans D. Mittelmann
2000-12-09
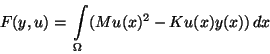
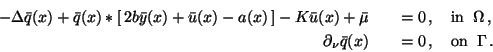
![]() , is even more
pronounced through the homogeneous Neumann conditions resulting in singular
constraints.
The largest instance has
, is even more
pronounced through the homogeneous Neumann conditions resulting in singular
constraints.
The largest instance has ![]() variables and
variables and ![]() constraints in the
NLP problem. These results were obtained on a HP9000-K260 with 256MB.
constraints in the
NLP problem. These results were obtained on a HP9000-K260 with 256MB.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() was solved.
The optimal control and state are shown in Figure 7.
Both the control and the state constraints become active.
The adjoint variable and the switching curves
was solved.
The optimal control and state are shown in Figure 7.
Both the control and the state constraints become active.
The adjoint variable and the switching curves ![]() displayed in Figure 8 admit a verification of the
control law (13).
While the CPU times for
displayed in Figure 8 admit a verification of the
control law (13).
While the CPU times for ![]() are excessive, the accuracy for
are excessive, the accuracy for ![]() should be sufficient and the times are acceptable. To avoid the trivial
solution
should be sufficient and the times are acceptable. To avoid the trivial
solution ![]() of the state equation nonzero starting values for the
state were chosen in this example. As in the case
of the state equation nonzero starting values for the
state were chosen in this example. As in the case ![]() , the local
optimality of the solution shown in Figure 7 would need to be verified.
, the local
optimality of the solution shown in Figure 7 would need to be verified.