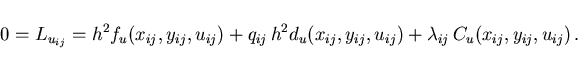

Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Discretization and optimization techniques
The discussion of discretization schemes is restricted to the standard
situation where
the domain is the unit square
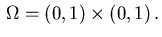 The purpose of this section is to develop discretization techniques by
which the distributed control
problem (2.1)-(2.6)
is transformed into a nonlinear programming problem (NLP-problem)
of the form
The purpose of this section is to develop discretization techniques by
which the distributed control
problem (2.1)-(2.6)
is transformed into a nonlinear programming problem (NLP-problem)
of the form
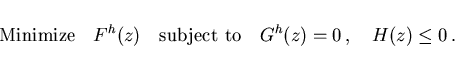 |
(3.1) |
The functions 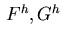 and
and 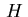 are sufficiently smooth and are of
appropriate dimension.
The upper subscript
are sufficiently smooth and are of
appropriate dimension.
The upper subscript 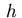 denotes the dependence on the stepsize.
The optimization variable
denotes the dependence on the stepsize.
The optimization variable 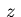 will comprise both the
discretized state and control variables.
will comprise both the
discretized state and control variables.
The form (3.1) will be achieved by solving
the elliptic equation (2.2)
with the standard five-point-star discretization scheme.
Choose a number
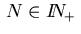 and the stepsize
and the stepsize
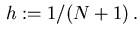 Consider the mesh points
Consider the mesh points
and define the following sets of indices 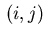 residing either in the domain
residing either in the domain 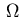 or on
the boundary
or on
the boundary 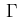 , resp. on the subsets
, resp. on the subsets
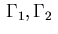 of the boundary:
of the boundary:
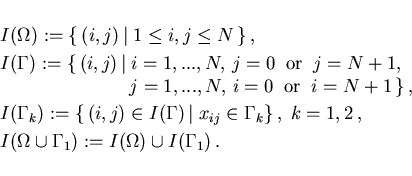 |
(3.2) |
Obviously, we have
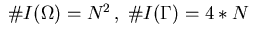 ;
define further
;
define further
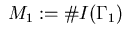 .
.
Now we shall present discretization schemes for the
distributed control problem that are similar to those for boundary controls
considered in Part 1 [23].
The optimization variable 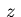 in (3.1) is taken as the vector
in (3.1) is taken as the vector
The remaining state variables
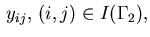 are
are determined by the Dirichlet condition (2.4) as
are
are determined by the Dirichlet condition (2.4) as
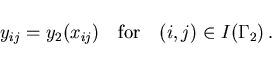 |
(3.3) |
The derivative
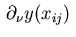 in the direction of
the outward normal is approximated by the expression
in the direction of
the outward normal is approximated by the expression
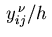 where
where
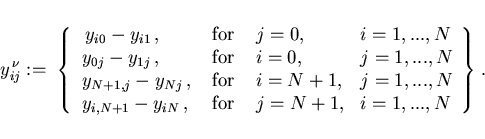 |
(3.4) |
Then the discrete form of the Neumann boundary condition (2.3)
leads to the equality constraints
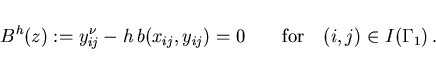 |
(3.5) |
The application of the five-point-star to the
elliptic equation
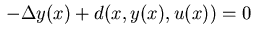 in (2.2) yields the following equality constraints for all
in (2.2) yields the following equality constraints for all
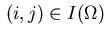 :
:
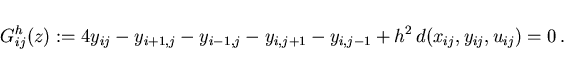 |
(3.6) |
Note that the Dirichlet condition (3.3) is used in this equation to
substitute the variables 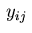 for
for
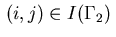 .
The control and state inequality constraints (2.5) and
(2.6) yield the inequality constraints
.
The control and state inequality constraints (2.5) and
(2.6) yield the inequality constraints
| |
|
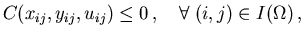 |
(3.7) |
| |
|
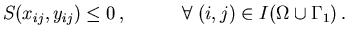 |
(3.8) |
Observe that these inequality constraints do not depend on the
meshsize 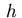 .
The discretized form of the cost function (2.1) is
.
The discretized form of the cost function (2.1) is
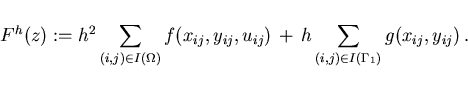 |
(3.9) |
In summary, the relations (3.5)-(3.9) define
a NLP-problem of the form (3.1).
The corresponding Lagrangian function is
where the Lagrange multipliers
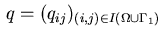 ,
,
 and
and
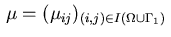 are associated with
the equality constraints (3.5) and (3.6),
resp. the inequality constraints (3.7) and (3.8).
In addition, the multipliers
are associated with
the equality constraints (3.5) and (3.6),
resp. the inequality constraints (3.7) and (3.8).
In addition, the multipliers 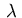 and
and 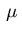 satisfy
the complementarity conditions corresponding to (2.14):
satisfy
the complementarity conditions corresponding to (2.14):
In the next step we discuss the necessary conditions of optimality:
For state variables 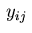 with indices
with indices
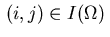 we obtain the relations
we obtain the relations
In these equations, the up to now undefined multipliers are set to
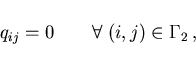 |
(3.12) |
which is in accordance with the Dirichlet condition (2.12).
We deduce from equations (3.11) that the Lagrange multipliers
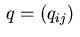 satisfy the five-point-star difference equations
for the adjoint equation
satisfy the five-point-star difference equations
for the adjoint equation
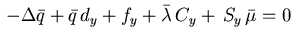 in (2.10)
if we use the following approximations for the multiplier function
in (2.10)
if we use the following approximations for the multiplier function
 and
the regular Borel measure
and
the regular Borel measure  ,
,
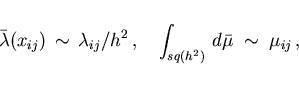 |
(3.13) |
where in the second relation
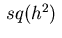 denotes a square centered at
denotes a square centered at 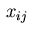 with area
with area 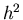 .
Recall the decomposition (2.15) of the measure
.
Recall the decomposition (2.15) of the measure
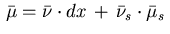 .
If the singular part of the measure vanishes,
i.e.
.
If the singular part of the measure vanishes,
i.e.
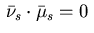 holds,
then (3.13) yields the following
approximation for the density
holds,
then (3.13) yields the following
approximation for the density 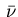 ,
,
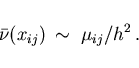 |
(3.14) |
In case that the measure
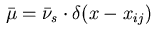 is a delta distribution,
we obtain from (3.13) the approximation
is a delta distribution,
we obtain from (3.13) the approximation
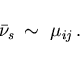 |
(3.15) |
For indices
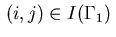 on the boundary
on the boundary 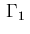 ,
e.g., for
,
e.g., for
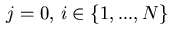 , we obtain
, we obtain
These relations represent the discrete version of the Neumann boundary condition (2.11) if we approximate the regular
Borel measure 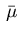 on the boundary by
on the boundary by
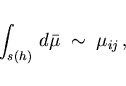 |
(3.16) |
where 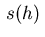 denotes a line segment of length
denotes a line segment of length 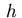 on
on
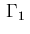 centered at
centered at 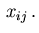 If the singular part in the decomposition (2.15) vanishes resp.
if the measure
If the singular part in the decomposition (2.15) vanishes resp.
if the measure
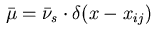 is a delta distribution,
we obtain the following approximations
is a delta distribution,
we obtain the following approximations
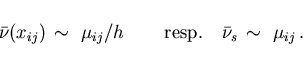 |
(3.17) |
Finally, necessary conditions with respect to the control variables
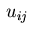 for
for
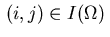 are determined by
are determined by
From this equation we recover the discrete version of the control law
(2.13), if we use the same identification
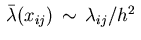 as in (3.13).
as in (3.13).


Next: Optimization codes and modeling
Up: Discretization and optimization techniques
Previous: Discretization and optimization techniques
Hans D. Mittelmann
2000-10-06
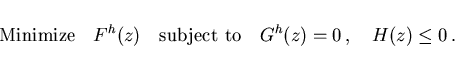
![]() and the stepsize
and the stepsize
![]() Consider the mesh points
Consider the mesh points
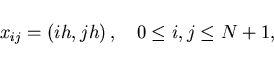
![]() in (3.1) is taken as the vector
in (3.1) is taken as the vector
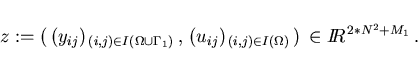
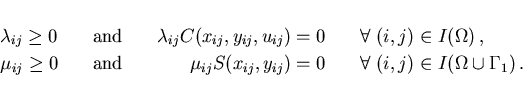
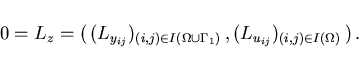
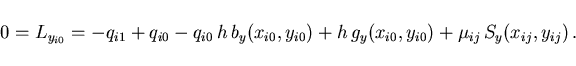
![]() for
for
![]() are determined by
are determined by