

Next: Discretization and optimization techniques
Up: Necessary conditions for elliptic
Previous: Boundary control problem
Here the problem is to determine a distributed control function
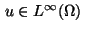 that minimizes the functional
that minimizes the functional
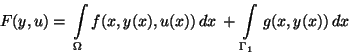 |
(25) |
subject to the elliptic state equation,
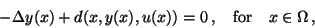 |
(26) |
Neumann and Dirichlet boundary conditions,
and mixed control-state inequality constraints resp. pure
state inequality constraints,
| |
|
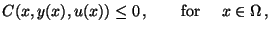 |
(29) |
| |
|
 |
(30) |
The functions
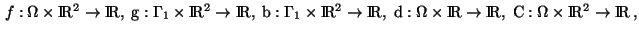 and
and
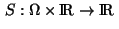 are assumed to be
are assumed to be 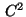 -functions,
while the Dirichlet condition (28) holds with
-functions,
while the Dirichlet condition (28) holds with
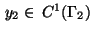 .
.
The above distributed control problem is slightly more general than the one
considered in Bonnans and Casas [9] where first order
conditions have been given in terms of a weak and strong Pontryagin principle.
For linear elliptic equations, first order conditions may also
be found in Bergounioux et al. [3], Bonnans and Casas
[8].
Nonlinear elliptic equations of Lotka-Volterra type have been treated in
Canada et al. [12] and Leung, Stojanovic [25,34].
Denote an optimal solution of problem (25)-(30)
by 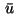 and
and 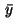 .
The active sets corresponding to the inequality constraints
(29), (30) are given by
.
The active sets corresponding to the inequality constraints
(29), (30) are given by
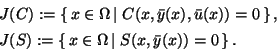 |
(31) |
It is required that the following regularity conditions
analogous to (8) hold:
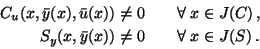 |
(32) |
Then first order necessary conditions can be stated in the following form.
There exist an adjoint state
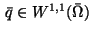 ,
a multiplier
,
a multiplier
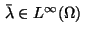 and a regular Borel measure
and a regular Borel measure 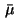 in
in 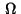 such that the following conditions hold:
such that the following conditions hold:
adjoint equation and boundary conditions:
minimum condition for
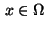 :
:
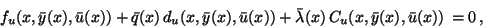 |
(36) |
complementarity conditions:
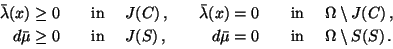 |
(37) |
The adjoint equations (33)-(35) are understood
in the weak sense.
The regular Borel measure
in the adjoint equation (33) has a decomposition
similar to that in (15),
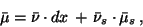 |
(38) |
where 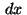 represents the Lebesgue measure and the measure
represents the Lebesgue measure and the measure
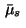 is singular
with respect to
is singular
with respect to 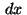 .
.
With regard to Example 4.2 in section 4 we shall discuss the minimum condition
(36) in case that the control and state constraints (29) and (30) are box constraints
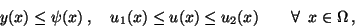 |
(39) |
with functions
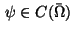 and
and
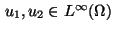 .
We immediately derive from (36) the control law
.
We immediately derive from (36) the control law
![\begin{displaymath}
\begin{array}{l}
[\,f_u(x,\bar{y}(x),\bar{u}(x)) + \bar{q}(x...
...ll \; u \in [u_1(x),u_2(x)] \,, \; x \in \Omega \,.
\end{array}\end{displaymath}](img111.gif) |
(40) |
It is straightforward to obtain analogous control laws
for tracking functionals similar to (16).


Next: Discretization and optimization techniques
Up: Necessary conditions for elliptic
Previous: Boundary control problem
Hans D. Mittelmann
2000-12-09
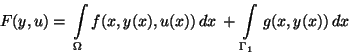
![]() and
and ![]() .
The active sets corresponding to the inequality constraints
(29), (30) are given by
.
The active sets corresponding to the inequality constraints
(29), (30) are given by