

Next: The optimization problem
Up: No Title
Previous: Introduction
Let 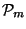 and
and
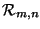 respectively denote the linear space of all
polynomials of degree
respectively denote the linear space of all
polynomials of degree 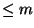 and the set of all rational functions
with numerator degree
and the set of all rational functions
with numerator degree 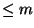 and denominator degree
and denominator degree 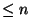 ;
furthermore, denote by
fk the interpolated values f(xk), k=0(1)N, of f.
Then the unique polynomial
;
furthermore, denote by
fk the interpolated values f(xk), k=0(1)N, of f.
Then the unique polynomial
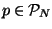 that interpolates f between
the xk's
can be written in its barycentric form [12]
that interpolates f between
the xk's
can be written in its barycentric form [12]
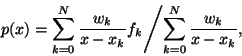 |
(1) |
where the so-called weight wk corresponding to the point xkis given by
The barycentric formula has several advantages [18], [6, p. 357].
One of them is
the fact that the weights appear in the numerator and in the denominator,
so that
they can be divided by any common factor. For example, simplified weights
for equidistant points are given by
[8], while for the
Cebysevpoints of the second kind
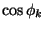 ,
,
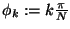 ,
one simply has [17]
,
one simply has [17]
As explained in the introduction, we now want to improve the quality of
approximation of the interpolant, for instance for functions with very large
derivatives. For that purpose, we will divide the interpolant by an optimized
denominator, while maintaining interpolation.
Let P, 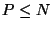 ,
be the number of poles zi, i=1(1)P, we want
to attach to the polynomial. If some rational interpolant
,
be the number of poles zi, i=1(1)P, we want
to attach to the polynomial. If some rational interpolant
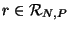 exists with poles at the zi's and only there, then
its denominator takes the values
exists with poles at the zi's and only there, then
its denominator takes the values
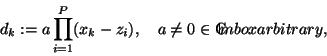 |
(2) |
at the interpolation points xk.
(The fact that it does not exist may mean that attaching the poles is not
advisable
from an approximation point of view, see [4].)
To insure interpolation, the values of the numerator at the same points
will be fkdk. Writing the numerator and the denominator as interpolating
polynomials in their barycentric form (1) and simplifying, one gets
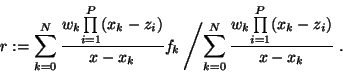 |
(3) |
(3) is the barycentric representation of rwith weights
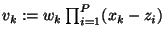 .
In the present case, with all poles prescribed, the weights are unique up to
a constant [4].
Barycentric representations exist for every rational interpolant
in
.
In the present case, with all poles prescribed, the weights are unique up to
a constant [4].
Barycentric representations exist for every rational interpolant
in
 [5], and computing them is a way of solving the classical rational
interpolation
problem also when only a subset of the poles are prescribed [4].
[5], and computing them is a way of solving the classical rational
interpolation
problem also when only a subset of the poles are prescribed [4].
In order to stay with real interpolants, we will assume here
that the poles zi with
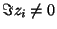 arise in complex conjugate
pairs.
arise in complex conjugate
pairs.


Next: The optimization problem
Up: No Title
Previous: Introduction
Hans Mittelmann
2000-05-30
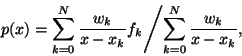
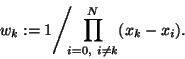
![]() ,
be the number of poles zi, i=1(1)P, we want
to attach to the polynomial. If some rational interpolant
,
be the number of poles zi, i=1(1)P, we want
to attach to the polynomial. If some rational interpolant
![]() exists with poles at the zi's and only there, then
its denominator takes the values
exists with poles at the zi's and only there, then
its denominator takes the values
![]() arise in complex conjugate
pairs.
arise in complex conjugate
pairs.