Bibliography

1

L. Ahlfors, Complex Analysis, 2nd ed., McGraw-Hill, New York, 1966.

2

K. E. Atkinson, An Introduction to Numerical Analysis, 2nd ed., John Wiley, New York, 1978.

3

R. Baltensperger and J.-P. Berrut, The linear rational collocation method, to appear in J. Comput. Appl. Math.

4

J.-P. Berrut, The barycentric weights of rational interpolation with prescribed poles, J. Comput. Appl. Math. 86 (1997), 45-52.

5

J.-P. Berrut and H. Mittelmann, Lebesgue constant minimizing linear rational interpolation of continuous functions over the interval, Computers Math. Applic. 33 (1997), 77-86.

6

J.-P. Berrut and H. Mittelmann, Matrices for the direct determination of the barycentric weights of rational interpolation, J. Comput. Appl. Math. 78 (1997), 355-370.

7

J.-P. Berrut and H. Mittelmann, The linear rational collocation method with iteratively optimized poles for two-point boundary value problems, submitted for publication.

8

R. Bulirsch and H. Rutishauser, Interpolation und genäherte Quadratur, Sauer R., Szabó I., Hsg., Mathematische Hilfsmittel des Ingenieurs, Grundlehren der math. Wissenschaften Bd. 141, Springer, Berlin-Heidelberg, 1968, pp. 232-319.

9

A. Corana, M. Marchesi, C. Martini, and S. Ridella, Minimizing multimodal functions of continuous variables with the ``Simulated Annealing'' algorithm, ACM Trans. Math. Software 13 (1987), 262-280.

10

P. R. Graves-Morris, Efficient reliable rational interpolation, in: Padé Approximation and its Applications, Amsterdam, 1980 M. G. de Gruin and H. van Rossum, eds., LNM 888, Springer-Verlag, Berlin-Heidelberg-New York, 1981, pp. 28-63.

11

P. Hemker, A Numerical Study of Stiff Two-Point Boundary Problems, Math. Centrum, Amsterdam, 1977.

12

P. Henrici, Essentials of Numerical Analysis, John Wiley, New York, 1982.

13

P. Henrici, Applied and Computational Complex Analysis, Vol. 1, John Wiley, New York, 1974.

14

E. H. Kaufman, Jr., D. J. Leeming, and G. D. Taylor, Uniform rational approximation by differential correction and Remes-differential correction, Int. J. Numer. Meth. Engin. 17 (1981), 1273-1278.

15

Matlab Robust Control User's Guide, The Mathworks Inc., Natick MA, 1999.

16

T. J. Rivlin, An Introduction to the Approximation of Functions, Dover, 1981.

17

H. E. Salzer, Lagrangian interpolation at the Chebyshev points 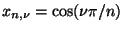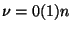$x_{n,\nu} = \cos(\nu\pi/n)$, $\nu=0(1)n$; some unnoted advantages, The Computer J. 15 (1972), 156-159.

18

C. Schneider, W. Werner, Some new aspects of rational interpolation, Math. Comp. 47 (1986), 285-299.

19

J. Stoer, Einführung in die Numerische Mathematik I, 4. Aufl., Springer, Berlin, 1972.

20

H. Werner, Algorithm 51: A reliable and numerically stable program for rational interpolation of Lagrange data, Computing 31 (1983), 269-286.

21

J. L. Zhou, A. L. Tits and C. T. Lawrence, User's guide for FFSQP version 3.7: A FORTRAN code for solving optimization problems, possibly minimax, with general inequality constraints and linear equality constraints, generating feasible iterates, TR-92-107r5, Institute for Systems Research, University of Maryland, College Park, MD20742, USA, 1997.