


Next: Application Problems
Up: Interior Point Methods for
Previous: Introduction and Definitions
In this section, we prove the existence
of the step length 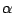 using the method described in
[18]. See also [11] for an analysis of the semidefinite case.
Here is the algorithm which we analyze in this section.
using the method described in
[18]. See also [11] for an analysis of the semidefinite case.
Here is the algorithm which we analyze in this section.
Algorithm 2.1
Given
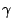
,
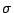
,

for

Set

Solve (
1-6) for
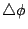
Find the largest
![$ \alpha\in [0,1]$](img95.gif)
, such that

Update

end.
Denote the maximal and minimal eigenvalues of 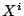 by
by
 and
and
 ,
respectively. From [9], we have that
Since
,
respectively. From [9], we have that
Since  is
the diagonal matrix consisting of
is
the diagonal matrix consisting of
 , it follows
that
, it follows
that
 and
and
 are
obtained from
are
obtained from
We now start to find upper bounds for vectors. We consider
Algorithm 2.1, but we use (1-6) with the
NT direction instead of (1-5).
First, we introduce a useful quantity  defined by
defined by
 |
(2-1) |
where  is the step length and
is the step length and  is the
centering parameter in the
is the
centering parameter in the 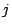 -th iteration. According to Lemma
3.13 in [4] and the definitions of
-th iteration. According to Lemma
3.13 in [4] and the definitions of
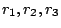 in
Algorithm 2.1, we have
We choose the initial point by the following:
in
Algorithm 2.1, we have
We choose the initial point by the following:
 |
(2-2) |
where
 The
following lemma gives the bound on
The
following lemma gives the bound on
Lemma 2.2
Let the initial point be given by (
2-2). For all

, there exists

, such that
Proof.
For simplicity, we ignore the
iteration index

on the vectors. Let

be any primal-dual
solution and define
It is easy to verify that

satisfies the following three equations:
 |
(2-3) |
Hence,
 |
(2-4) |
From (
2-4), we have
 |
(2-5) |
Since

is self-dual and

is a solution, we
have that
After inserting the above equations into (
2-5), we obtain
the following inequality,
Next, we define the constant

by
where

are the first two entries of

By (
2-2), we have that

One can also
derive the following inequality based on the definition of the
initial point,
Therefore,
Since

,
Furthermore, because

it
follows that
Since we specifically discuss the system (1-6) with
the NT search direction, we define the following notation for the
scaled vectors at the 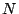 -th iteration:
The next lemma
gives bounds on the scaled vectors
-th iteration:
The next lemma
gives bounds on the scaled vectors
 and
and

Lemma 2.3
Applying the NT scaling scheme to (
1-6), i.e., using

, there is a positive constant

, such that
Proof.
Let us define
It is easy to verify that

satisfies (
2-3)
and (
2-4). In order to obtain the fourth equation in
(
1-6), we use the following expression
Since we consider the NT direction, i.e.,

, we
multiply by

from the left and obtain
Similarly,
We now consider the 2-norm of the vector,
On the other hand,
Combining the above two observations, we obtain an upper bound,
We now need to show that each term in the right hand side of the
above inequality is

First, we consider

From the property of

and the
definition of

, we derive
Hence,
Thus,
For the remaining terms in the inequality, we have
 |
(2-6) |
Since

max

, we find upper bounds for

and

So,
since

Thus,
Now (
2-6) is bounded by

max

Hence,
If the initial point satisfies (2-2), then the next
lemma follows immediately.
Lemma 2.4
Under the same conditions as in the previous lemma and if the
initial point satisfies the (
2-2), then

and

Proof.
From(
2-2), we have that
where
![$ e_1=[1,\cdots,1]^T.$](img184.gif)
Then, we can derive the
following two estimates,
It is easy to check that
The next lemma shows the existence of the step length 
Lemma 2.5
There exists
![$ \bar\alpha\in [0,1]$](img188.gif)
such that

for all
![$ \alpha\in [0,\bar\alpha],$](img190.gif)
where

is defined as

Proof.
For simplicity, we consider the quadratic cone case
only. By Lemma
2.4, we have
From
the last two equations of the system (
1-6), we
obtain
In order to consider

we estimate

by
We now consider the conditions of

. We note that
If
holds, then
Therefore,
 min min |
(2-7) |
A similar result in [9] is based on feasible initial
points, however, the condition (2-7) is good for
infeasible initial points.



Next: Application Problems
Up: Interior Point Methods for
Previous: Introduction and Definitions
Hans D. Mittelmann
2003-09-10
![]() defined by
defined by





 for all
for all 








 max
max

 and
and 





