


Next: Existence of step length
Up: Interior Point Methods for
Previous: Interior Point Methods for
Over the past few years, primal-dual
interior point methods (IPM) have been developed for all kinds of
nonlinear optimization problems. Second-order cone programming
(SOCP) is one of these. SOCP addresses the problem of minimizing a
linear objective function over the intersection of an affine set
and the direct product of quadratic cones. Numerous applications
have been discussed in [5,15]. Recently, many reseachers have
shown that the primal-dual IPM has high theoretical efficiency for
SOCP. In particular, Tsuchiya [13] and Monteiro and Tsuchiya
[9] have proved the complexity of variants of IPMs based on
different scaling directions. Specifically, Tsuchiya [13]
shows that the long-step path-following algorithm using the
Nesterov and Todd (NT) direction has
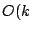 log
log
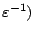 iteration complexity which is also the best
result for the scaling methods they considered.
iteration complexity which is also the best
result for the scaling methods they considered.
In this section we introduce the second order problem (SOCP) and
quote some basic definitions for the primal-dual interior point
approach. The next section contains as on of the main results a
proof of the existence of the step length for the long-step
method. A number of applications and in each case their
reformulation as SOCP is presented in section 3. Subsequently, the
various algorithms we have implemented are given in detail and
compared on a test set derived from the application problems. We
conclude with a summary in the last section.
Second-order cone programming addresses the problem of minimizing
a linear objective function over the intersection of an affine set
and the direct product of quadratic cones.
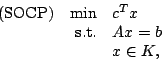 |
(1-1) |
where K is a closed convex cone. In addition to (1-1), we
suppose 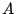 is a
is a 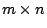 real matrix and of full
rank. Subsequently, the dual problem is
real matrix and of full
rank. Subsequently, the dual problem is
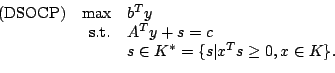 |
(1-2) |
The definition of the quadratic cone  is the following:
is the following:
Definition 1.1
The second order cone

is defined as,
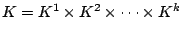
, i.e., the direct product of
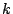
cones, where
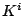
is one of the three cones below,
-
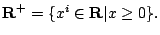
- quadratic cone
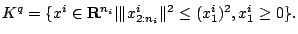
- rotated quadratic cone
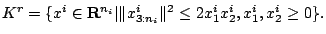
Note that  Moreover, there is a linear transformation
Moreover, there is a linear transformation 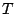 between
between 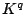 and
and 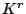 such that
where
such that
where
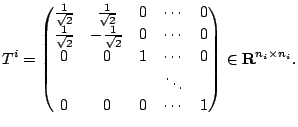 |
(1-3) |
Here, 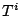 is a
is a
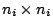 identity matrix if
identity matrix if
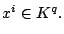 The existence of the linear transformation
The existence of the linear transformation 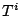 not only
extends the problem to rotated quadratic cones but also helps to
apply the convergence theorem for
not only
extends the problem to rotated quadratic cones but also helps to
apply the convergence theorem for 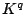 to
to 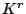 .
Next, we partition
.
Next, we partition 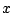 according to the cones, i.e.,
We introduce two nonnegative scalar variables
according to the cones, i.e.,
We introduce two nonnegative scalar variables
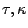 and
define the general Goldman-Tucker homogeneous model as follows:
and
define the general Goldman-Tucker homogeneous model as follows:
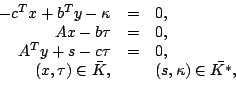 |
(1-4) |
where
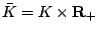 , and
, and
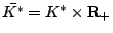 . In
order to solve (1-4) with the complementarity conditions,
the following definitions are necessary,
. In
order to solve (1-4) with the complementarity conditions,
the following definitions are necessary,
Next, we define  for each type of cone:
for each type of cone:
Subsequently, the complementarity conditions can be written as a
nonlinear system.
Lemma 1.4
Let
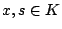
, then
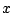
and
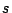
are complementary, i.e.,
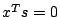
, if and only if
where
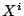
and
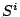
are given in Definition
1.3.
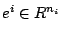
is the first unit vector.
See [1] for proof. An
initial point
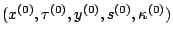 is given by
Thus, the central path can be defined as:
is given by
Thus, the central path can be defined as:
Definition 1.5
The points
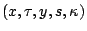
of the central path
are
defined by the following nonlinear
equations,
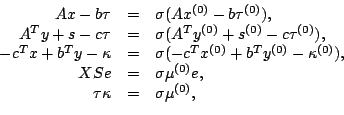 |
(1-5) |
where the centering parameter
![$ \sigma\in [0,1]$](img57.gif)
, the duality
measure is
,
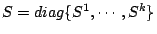
, and
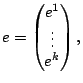
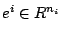
is the first unit vector.
There are different ways to define the neighborhood. We choose the
one similar to
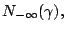
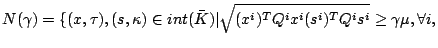
and
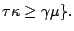
In the
original infeasible interior point method, the residuals only
appear in equations after applying Newton's method. It is easy to
verify that the ratio between the new and old residual is
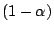 , where
, where 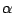 is the step length. It is faster than
the rate at which the complementarity gap decreases. This central
path gives the same rate for infeasibility and the complementary
gap. In experiments, we see the latter version needs less
iterations than the previous one.
is the step length. It is faster than
the rate at which the complementarity gap decreases. This central
path gives the same rate for infeasibility and the complementary
gap. In experiments, we see the latter version needs less
iterations than the previous one.
The well-definedness of (1-5) is not guaranteed.
One way to assure that the search direction is well-defined is
applying scaling schemes before using Newton's method, then
scaling back to the original space. Next, we give the definition
of scaling matrices,[1].
The scaled point
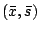 is defined by the
transformation
is defined by the
transformation
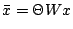
and
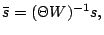
where
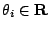 , and
, and 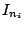 is the identity matrix
is the identity matrix
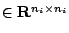 , for all
, for all 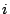 . It is easy to see that
. It is easy to see that
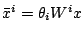 , and
, and
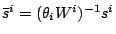 .
Therefore, the
linear system for the scaled search direction is defined by
.
Therefore, the
linear system for the scaled search direction is defined by
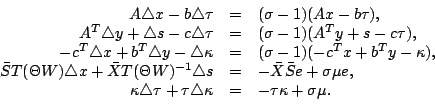 |
(1-6) |
The NT direction was proposed by Nesterov and Todd [10]. The
paper [10] also shows that the primal-dual IPM maintains its
efficiency when the nonnegative constraints in LP are replaced by
the homogeneous self-dual cone. More recently, Tsuchiya [13]
showed that the long-step algorithm for SOCP using NT direction
has
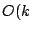 log
log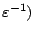 , iteration-complexity, where
, iteration-complexity, where
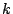 is the number of cones, which is the best result among several
scaling schemes.
is the number of cones, which is the best result among several
scaling schemes.
The NT direction defines  , and
, and 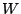 , such
that
, such
that
Hence,
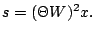 The definitions of
The definitions of  and
and 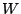 are given
in the following lemma. See [13] for the uniqueness.
are given
in the following lemma. See [13] for the uniqueness.
To simplify notations through out this paper, we define the
following symbols.
Definition 1.7
Define
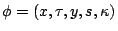
,
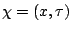
and
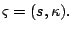



Next: Existence of step length
Up: Interior Point Methods for
Previous: Interior Point Methods for
Hans D. Mittelmann
2003-09-10

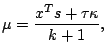
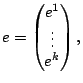
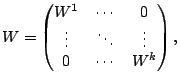
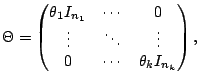
![]() log
log![]() , iteration-complexity, where
, iteration-complexity, where
![]() is the number of cones, which is the best result among several
scaling schemes.
is the number of cones, which is the best result among several
scaling schemes.
![]() , and
, and ![]() , such
that
, such
that