

Next: The test example
Up: First and second-order optimality
Previous: First order necessary conditions
Let
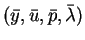 be given such that the system of first order
necessary conditions is satisfied, i.e. the relations (1.2-1.4),
(2.2-2.4) and
be given such that the system of first order
necessary conditions is satisfied, i.e. the relations (1.2-1.4),
(2.2-2.4) and
 are fulfilled. Now we state
second order conditions, which imply local optimality of
are fulfilled. Now we state
second order conditions, which imply local optimality of 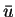 .
For this purpose, we need the second order derivative of
.
For this purpose, we need the second order derivative of 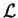 with respect to
with respect to 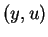 ,
,
![\begin{displaymath}
{\cal L}''(\bar{y},\bar{u},\bar{p},\bar{\lambda}) [y,u]^2= \...
..._0^T u^2\, dt + 2 \int \limits_0^T \bar{p}(l,t) y^2(l,t)\,
dt. \end{displaymath}](img50.gif) |
(2.6) |
Let us assume as in the example below that the state-constraint
(1.4) is active at 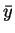 and
and
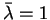 . Then we require the
following second-order sufficient optimality condition:
. Then we require the
following second-order sufficient optimality condition:
(SSC) There exist positive 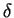 and
and 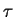 such that
such that
![\begin{displaymath}
{\cal L}''(\bar{y},\bar{u},\bar{p},\bar{\lambda}) [y,u]^2 \ge \delta\, \int \limits_0^T
u^2\, dt \end{displaymath}](img54.gif) |
(2.7) |
holds for all
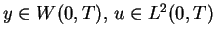 such that
such that
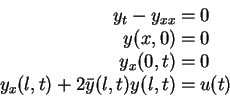 |
(2.8) |
and
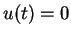 |
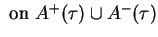 |
|
(2.9) |
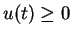 |
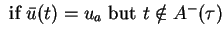 |
|
(2.10) |
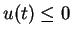 |
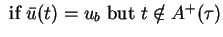 |
|
(2.11) |
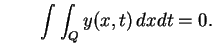 |
|
|
(2.12) |
It is known that (SSC) implies local optimality of 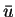 in a neighborhood
of
in a neighborhood
of 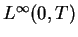 , see [4]. In our example, we shall verify
a slightly stronger condition. We require (2.7) for all
, see [4]. In our example, we shall verify
a slightly stronger condition. We require (2.7) for all 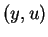 , which
satisfy only (2.8-2.9).
, which
satisfy only (2.8-2.9).


Next: The test example
Up: First and second-order optimality
Previous: First order necessary conditions
Hans D. Mittelmann
2003-01-25
![]() be given such that the system of first order
necessary conditions is satisfied, i.e. the relations (1.2-1.4),
(2.2-2.4) and
be given such that the system of first order
necessary conditions is satisfied, i.e. the relations (1.2-1.4),
(2.2-2.4) and
![]() are fulfilled. Now we state
second order conditions, which imply local optimality of
are fulfilled. Now we state
second order conditions, which imply local optimality of ![]() .
For this purpose, we need the second order derivative of
.
For this purpose, we need the second order derivative of ![]() with respect to
with respect to ![]() ,
,
![]() and
and ![]() such that
such that