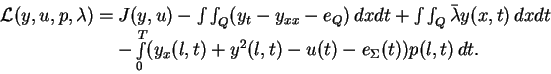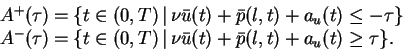

Next: Second order sufficient optimality
Up: First and second-order optimality
Previous: First and second-order optimality
Let the control 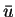 be locally optimal for (P) with associated state
be locally optimal for (P) with associated state 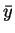 ,
i.e.
,
i.e.
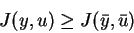 |
(2.1) |
holds for all 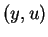 satisfying the constraints (1.2-1.4),
where
satisfying the constraints (1.2-1.4),
where 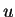 belongs to a sufficiently small
belongs to a sufficiently small 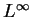 -neighborhood of
-neighborhood of
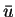 . Suppose further that
. Suppose further that
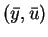 is regular. Then there exist
Lagrange multipliers
is regular. Then there exist
Lagrange multipliers
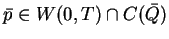 (the
adjoint state) and
(the
adjoint state) and
 such that the adjoint
equation
such that the adjoint
equation
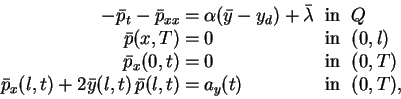 |
(2.2) |
the variational inequality
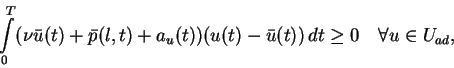 |
(2.3) |
and the complementary slackness condition
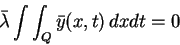 |
(2.4) |
are fulfilled, see [3] or [11]. We mention that (2.3)
is equivalent to the well-known projection property
![\begin{displaymath}
\bar{u}(t) = \Pi_{[u_a,u_b]}\{ -\frac{1}{\nu}(\bar{p}(l,t) + a_u(t))\},
\end{displaymath}](img35.gif) |
(2.5) |
where
![$\Pi_{[u_a,u_b]}: \mbox{\piz R}\rightarrow [u_a,u_b] $](img36.gif) denotes projection onto
denotes projection onto
![$[u_a,u_b]$](img37.gif) . Moreover, we recall that these conditions can be derived by
variational principles applied to the Lagrange function
. Moreover, we recall that these conditions can be derived by
variational principles applied to the Lagrange function 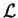 ,
,
Defining 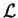 in this way, we tacitly assume that the homogeneous
initial and boundary conditions of
in this way, we tacitly assume that the homogeneous
initial and boundary conditions of 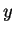 are formally included in the state
space. The conditions (2.2-2.3) follow from
are formally included in the state
space. The conditions (2.2-2.3) follow from
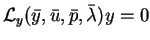 for all admissible increments
for all admissible increments 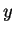 and
and
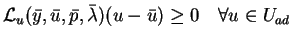 .
Let
.
Let 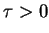 be given. We define
be given. We define
It holds 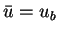 on
on 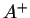 and
and 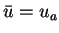 on
on  . These sets indicate
strongly active control constraints.
. These sets indicate
strongly active control constraints.


Next: Second order sufficient optimality
Up: First and second-order optimality
Previous: First and second-order optimality
Hans D. Mittelmann
2003-01-25
![]() be locally optimal for (P) with associated state
be locally optimal for (P) with associated state ![]() ,
i.e.
,
i.e.