


Next: Facility Location Problem (I)
Up: Application Problems
Previous: Application Problems
In this section, we will look at
the following model [2]:
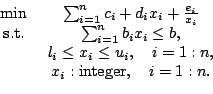 |
(3-1) |
This model can be interpreted as a multi-item production and
inventory management problem with a limited resource, where the
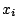 are called decision variables [17,20]. In general, the
objective function minimizes
the cost, which could be the sum of setup (ordering) costs,
inventory holding costs, and purchase costs. The constraints
provide the restrictions of a shared resource as well as
non-shared resources. Moreover, the model represents numerous
application problems based on the interpretations of the decision
variables. There are at least four different
applications using the model (3-1).
are called decision variables [17,20]. In general, the
objective function minimizes
the cost, which could be the sum of setup (ordering) costs,
inventory holding costs, and purchase costs. The constraints
provide the restrictions of a shared resource as well as
non-shared resources. Moreover, the model represents numerous
application problems based on the interpretations of the decision
variables. There are at least four different
applications using the model (3-1).
Let us consider the continuous relaxation of (3-1). In order
to solve it as a second-order cone problem, we must ensure that
(3-1) can be cast as SOCP. Let
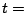 max
max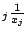 . Then
. Then
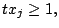 for all
for all 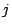 . We introduce a
. We introduce a
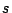 in this inequality and rewrite it as
in this inequality and rewrite it as
By using the following fact [5]:
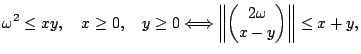 |
(3-2) |
the previous inequality becomes
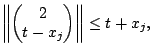
for all
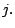
Therefore, we can rewrite the inequalities as
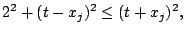
for all
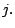
Next,
define 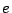 ,
, 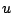 ,
,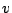 , and
, and 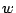 as follows,
as follows,
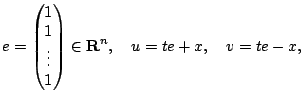
and
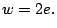
It is then clear that
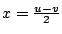 and
and
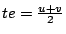 .
Plugging this into our model, we obtain
.
Plugging this into our model, we obtain
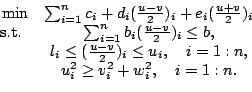 |
(3-3) |
In this form, the objective function and constraints, except the
last 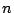 inequalities, are linear. Therefore, we can rewrite them
as LP. Each of the last
inequalities, are linear. Therefore, we can rewrite them
as LP. Each of the last 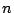 constraints is a quadratic cone with
constraints is a quadratic cone with
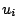 ,
, 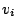 , and
, and 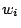 . We use the random problems described in
[2] to generate test cases.
. We use the random problems described in
[2] to generate test cases.
Example 1. Given
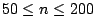 ,
,
![$ S_i\in [5,20]$](img227.gif) ,
,
![$ H_i\in [1,4]$](img228.gif) ,
,
![$ D_i\in [10,100]$](img229.gif) ,
,
![$ T_i\in [1,15]$](img230.gif) ,
,
![$ l_i, u_i \in
[8,25]$](img231.gif) ,
,
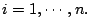 The total machine time available
The total machine time available  is
generated to ensure the feasibility of problems, i.e.,
is
generated to ensure the feasibility of problems, i.e.,
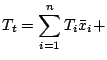
random positive number
where
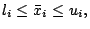 for all
for all  In Chapter 5, we
use Example 1 with
In Chapter 5, we
use Example 1 with
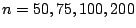 as part of our testing set.
as part of our testing set.



Next: Facility Location Problem (I)
Up: Application Problems
Previous: Application Problems
Hans D. Mittelmann
2003-09-10
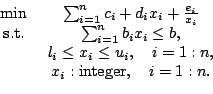
![]() max
max![]() . Then
. Then
![]() for all
for all ![]() . We introduce a
. We introduce a
![]() in this inequality and rewrite it as
in this inequality and rewrite it as
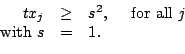
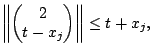 for all
for all 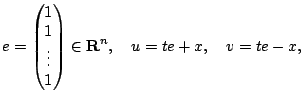 and
and ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() The total machine time available
The total machine time available ![]() is
generated to ensure the feasibility of problems, i.e.,
is
generated to ensure the feasibility of problems, i.e.,
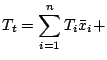 random positive number
random positive number