


Next: Facility Location Problem (II)
Up: Application Problems
Previous: Management Problem
This problem is given as follows:
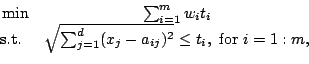 |
(3-4) |
where 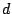 is the dimension,
is the dimension, 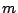 is the number of existing
facilities,
is the number of existing
facilities,
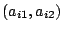 are the coordinates of the existing
facility (if
are the coordinates of the existing
facility (if 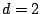 ), and
), and 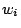 is the weight associated with the
old-new facility. The model describes that one plans to build a
new facility among existing facilities and chooses the location
which minimizes the weights associated with the Euclidean distance
between the new and existing locations. For simplicity, we
consider
is the weight associated with the
old-new facility. The model describes that one plans to build a
new facility among existing facilities and chooses the location
which minimizes the weights associated with the Euclidean distance
between the new and existing locations. For simplicity, we
consider 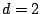 . It is trivial to extend to higher dimensions. Let
We then
introduce new linear constraints
Therefore, the problem becomes
. It is trivial to extend to higher dimensions. Let
We then
introduce new linear constraints
Therefore, the problem becomes
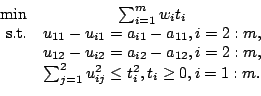 |
(3-5) |
We denote
and
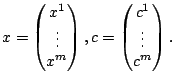 Hence, one obtains the SOCP formulation.
Hence, one obtains the SOCP formulation.
Example 2. The coordinates of the existing facilities and
the weight associated with each existing facility are both
generated by a uniform random number generator. We use
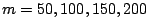 to create four problems.
to create four problems.



Next: Facility Location Problem (II)
Up: Application Problems
Previous: Management Problem
Hans D. Mittelmann
2003-09-10
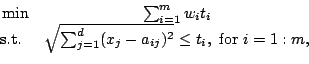
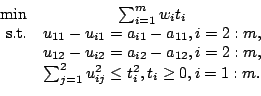
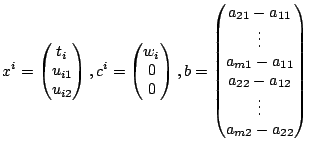
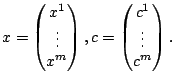 Hence, one obtains the SOCP formulation.
Hence, one obtains the SOCP formulation.
![]() to create four problems.
to create four problems.