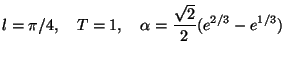 |
|||
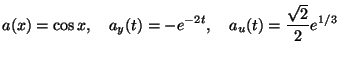 |
(5.1) | ||
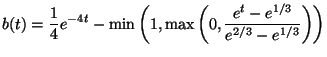 |
|||
In this section numerical results will be reported for the application of the method outlined in the previous section to three parabolic control problems from [1,9] and an exemplary elliptic control problems from [19]. The first parabolic problem is particularly interesting because for it in [1] an analytical exact solution is given and the continuous SSC conditions are verified. For the sake of completeness, the specification will be given for each problem. The discretizations used are those defined in section 2 for the parabolic and in [16]-[18] for the elliptic problem.
Problem (P) from section 2 is solved without state constraints
and with the following data
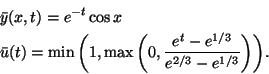
|
In Table 1
the maximum errors over the grid points are listed for
the computed control and state functions while in Table 2
the
smallest eigenvalue is listed as well as the value scaled by ![]() . The
errors exhibit quadratic convergence while the scaled eigenvalue stays
nearly constant with a slightly increasing tendency. These facts justify the
application of the technique to other control problems for which no exact
solution is known and it also shows which scaling of
. The
errors exhibit quadratic convergence while the scaled eigenvalue stays
nearly constant with a slightly increasing tendency. These facts justify the
application of the technique to other control problems for which no exact
solution is known and it also shows which scaling of ![]() is appropriate for
problem
is appropriate for
problem ![]() .
This scaling is also suggested by known quadratic convergence estimates for
fixed control in
.
This scaling is also suggested by known quadratic convergence estimates for
fixed control in ![]() since the differential equation as well as all
boundary conditions were discretized with second-order consistency.
An argument could be made that the smallness of the
eigenvalue may indicate that it is, in fact, negative and the relatively
coarse discretization prevents it from exhibiting this fact. This seems
highly unlikely in the light of the very uniform and even slightly
growing behavior of the scaled value combined with the fact that all
the eigenvalues were computed and the smallest one is not considerably
smaller than the next ones but they grow only gradually.
since the differential equation as well as all
boundary conditions were discretized with second-order consistency.
An argument could be made that the smallness of the
eigenvalue may indicate that it is, in fact, negative and the relatively
coarse discretization prevents it from exhibiting this fact. This seems
highly unlikely in the light of the very uniform and even slightly
growing behavior of the scaled value combined with the fact that all
the eigenvalues were computed and the smallest one is not considerably
smaller than the next ones but they grow only gradually.
As a second parabolic case one from [9] was chosen. The data for
(P) are
We include a plot of the optimal control and state for this problem.
Due to the consistent results obtained the computations for ![]() were not done in these cases.
were not done in these cases.
Finally, we solve a boundary control problem for the instationary
Burgers equation, see also [30]. For simplicity we used the
same data as for case (II) above with ![]() and the control bounds
and the control bounds
![]() both of which become active in the
solution. This case is denoted by 5.2-IV. It clearly shows that for
this problem the suitable normalization of the eigenvalue is
both of which become active in the
solution. This case is denoted by 5.2-IV. It clearly shows that for
this problem the suitable normalization of the eigenvalue is ![]() .
This will have to be confirmed by a careful comparison of the
continuous and discrete SSC as had been done for the first order
necessary conditions in [16,17]. A similar situation
arose in the elliptic boundary control problem in [18] which
is addressed next below. For it in [19] the scaling by
.
This will have to be confirmed by a careful comparison of the
continuous and discrete SSC as had been done for the first order
necessary conditions in [16,17]. A similar situation
arose in the elliptic boundary control problem in [18] which
is addressed next below. For it in [19] the scaling by ![]() seemed appropriate in contrast to the other such problems considered.
seemed appropriate in contrast to the other such problems considered.
Next, we present the data for the elliptic boundary control problem from
[18] and the eigenvalues obtained. The domain is the unit
square. The problem (EB) together with (2.1) and
(2.2) is considered and ![]() .
.
![\begin{eqnarray*}
&&d(x,y)\equiv0;\quad g(x,y,u)\equiv0;\quad b(x,y,u)=0,\quad\m...
...ma_2\\
&&y_d\equiv1,\quad\Omega_0=[.25,.75]^2,\quad \alpha=.005
\end{eqnarray*}](img96.gif)
We also include a plot of the optimal control and state for this problem. For plots of the adjoint variables and further details, we refer to [18].