The Unconstrained NLO Problem
The Problem: min f(x), n=dim(x)
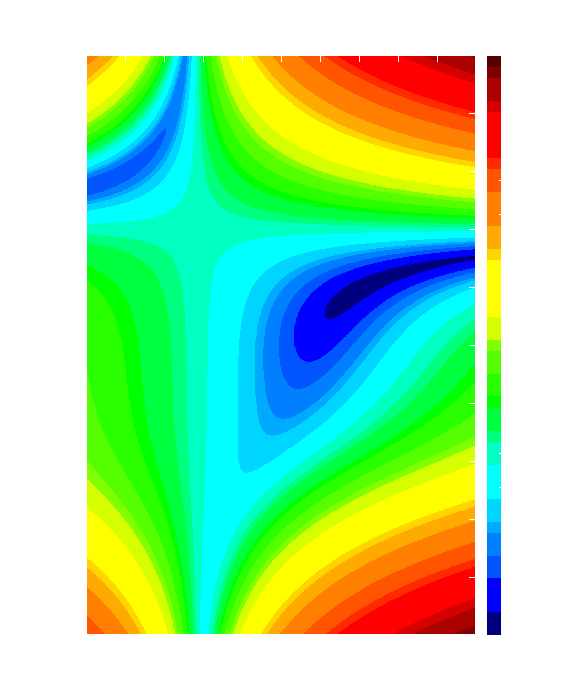
The picture shows the level set representation of Beale's testfunction
f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2.
It has a unique global minimizer at (3,0.5) and a saddle point at (0,1). There is a further saddle point at (0.100538,-2.644514).
For x=0 or y=1 it is constant with value 14.203125. In x<0 there exists an arc y(x)>0, where f decreases monotonically as x-> -INF.
Initial values near x=0 for large |y| or x<0, y>0 will let descent methods fail.
The methods listed here all restrict themselves to finding one solution of grad f(x)=0. For trust region based methods one often can show that this solution automatically satisfies the second order necessary conditions.
f is a "general" twice continuously differentiable function, but gradient is not available:
The methods implicitly all assume that f is twice continuously differentiable. They may fail or converge very slowly if this is not the case. Read M. Powell's and M. Wright's papers on Direct Search methods as well as M. Powell's paper on optimization without derivatives.
| VRBBO | Stochastic Matlab package with claims to near global optimization |
| FMIN | Fortran version of Brent's localmin (f77) |
| PRIMA | Updated implementation of MJD Powell's DFO codes in several languages |
| UNCMND | quasi-Newton method by Schnabel et al (f77) C++ version |
| WEDGE | Interpolation/trust region method for moderate dimensions(Matlab) |
| netlib/opt/praxis | f depends on few variables, the "principal axis method", tries to approximate the curvature of f |
| MCToolbox | three direct search methods incl Nelder-Mead, Matlab |
| nelmead | f depends on few variables, Nelder-Mead simplex-search method (no sound theoretical basis), f77 |
| netlib/opt/subplex | f depends on few variables, modification of the Nelder-Mead simplex-search method (no sound theoretical basis), (Matlab version) |
| fminsi | modified Nelder-Mead, LGPL-licensed, source, testdriver |
| HOPSPack | General derivative-free framework for unconstrained and linearly constrained problems, parallel, GPL, C++ |
f is only Lipschitz continuous or less: n not too large
| BFO | A trainable derivative-free solver for mixed-integer bound-constrained problems (Matlab) |
| GradSamp | Nonsmooth, nonconvex optimization by gradient sampling, by M. Overton et al; needs one of three QP solvers (Matlab) |
| LMBM | Limited Memory Bundle Method, f77, Matlab interface, testproblems, bound-constrained version |
| GRANSO | for nonsmooth, nonconvex optimization subject to nonsmooth, nonconvex constraints, based on a BFGS-SQP method (Matlab) |
| SolvOpt | Solves nonsmooth unconstrained and constrained problems of moderate dimensions (python). |
| OBOE | Oracle-Based Optimization Engine for convex problems, uses Proximal-ACCPM interior point method, C++ |
| PBUN/PNEW | Different f77 routines for Lipschitz continuous unconstrained and linearly constrained problems |
| NSO | various software for large-scale nonsmooth optimization (Fortran) |
| VXQR1 | Derivative-free unconstrained optimization based on QR factorizations (Matlab) |
The gradient of f is available or finite difference approximations are applicable :
n not too large (= some hundred say)
| netlib/toms/500 | the Shanno-Phua version of BFGS plus CG |
| netlib/toms/611 | trust region BFGS, this is a reliable and fairly efficient code. |
| netlib/toms/739 | tensor model quasi-Newton method, may be better for strongly nonquadratic f |
| NMTR | trust-region Newton, requires gradient |
| UCMINF | several methods, paper (Matlab) |
| CG_DESCENT | A new conjugate gradient method with guaranteed descent (f77/C) |
| csminwel | BFGS with some robustness against nonsmoothness (Matlab) |
f is convex differentiable, n large:
| netlib/opt/ve08 | f is a sum of convex differentiable functions each of which has considerably less variables than n (partially separable problem) (also for bound constraints), special quasi Newton method |
n large, f general, but not too wildly behaved :
| netlib/toms/630 updated version in f90 |
A combined limited memory qN/cg method (degrades for nonconvex f, nevertheless applicable; for ill-conditioned problem an individual preconditioner must be provided) |
| MINPACK-2 | A limited memory quasi Newton method. Directories contain software, drivers and manuals. (dcsrch.f, the step-size-algorithm, must be added; to be found e.g. in the following code) |
| LBFGS Java f90 |
a limited memory quasi Newton method using a new matrix representation; directory contains software, drivers and a user's manual. Not to be recommended for ill-conditioned problems. Add your own preconditioner! |
| LBFGS-B Matlab wrapper | needs C++ and Fortran compiler |
| CG+ | three basic cg methods, |
| POBLANO | Matlab toolbox |
| PREQN | preconditioning package |
| LM | Several limited memory f77-routines for unconstrained and box-constrained optimization; also for least squares |
n large, f strongly nonquadratic :
| netlib/opt/tn C-version |
Nash's truncated Newton method based on the Lanczos method, without explicit eigenvalue computation. takes directions of negative curvature into account. |
| netlib/toms/702 | truncated Newton based on the Lanczos process |
| TRON | trust region Newton, preconditioned cg, also for bound constraints |
f noisy :
| CMA-ES | Evolution Strategy with Covariance Matrix Adaptation (Matlab) |
| SNOBFIT | Stable Noisy Optimization by Branch and FIT (Matlab) |
| IMFIL | implicit filtering subject to box constraints and with multiple minima (Matlab) |
| DIRECT | the DIRECT algorithm (in Matlab) |
| VTDIRECT95 | Serial and Parallel Codes for the Global Optimization Algorithm DIRECT (Fortran 95) |
| netlib/opt/praxis | often applied to noisy problems although not directly designed for such |
| PRIMA | Updated implementation of MJD Powell's DFO codes in several languages |
| netlib/opt/subplex | f depends on few variables, modification of the Nelder-Mead simplex-search method (no sound theoretical basis), (Matlab version) |
f expensive to evaluate :
| RBFOpt | radial basis function library for black box (derivative free) optimization of functions with costly function evaluation (Python) |
| Scatter Search | all the C code from this book |
| SPACE | global optimization through meta-modeling: fitting, cross-validation, prediction, minimization etc (C++) |
| Spacemap | Optimization using Surrogate Models (Matlab) |
| STK | Matlab/Octave toolbox to construct a kriging approximation (surrogate) to computer models |
f complex :
| Complex Optimization Toolbox | MATLAB toolbox for optimization of complex variables |