


Next: Numerical realization and results
Up: Application Problems
Previous: FIR Filter Design
This
problem describes a mechanical system to find a hanging chain
consisting of 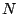 links. The first and last nodes are fixed. Each
node has a weight
links. The first and last nodes are fixed. Each
node has a weight 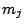 hanging from it. The problem is to
minimize the energy of the system (see [5,15]):
hanging from it. The problem is to
minimize the energy of the system (see [5,15]):
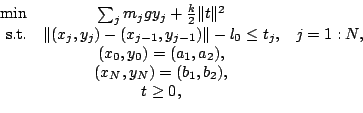 |
(3-10) |
where 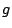 is the acceleration due to gravity,
is the acceleration due to gravity, 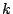 is the stiffness
constant of the springs,
is the stiffness
constant of the springs, 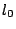 is the rest length of each spring,
and
is the rest length of each spring,
and 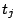 is an upper bound on the spring energy of the
is an upper bound on the spring energy of the 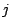 -th
spring. Consider
-th
spring. Consider
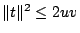 ,
, 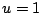 ,
, 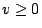 ,
,
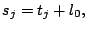 ,
,
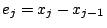 ,
,
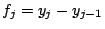 ,
, 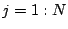 . Then
. Then
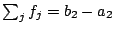 and
and
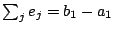 . The objective
function becomes
. The objective
function becomes
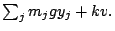 Furthermore,
The linear and cone constraints are
Furthermore,
The linear and cone constraints are
Example 6. The data is the same as in springs.mod in
[16]. We have 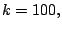
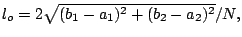
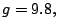
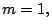
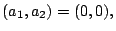 and
and
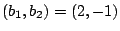 . We use
. We use
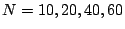 as test cases.
as test cases.
Hans D. Mittelmann
2003-09-10
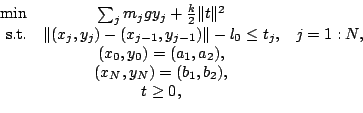
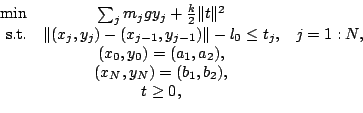
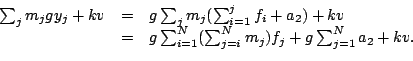
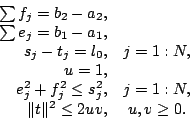
![]()
![]()
![]()
![]()
![]() and
and
![]() . We use
. We use
![]() as test cases.
as test cases.