


Next: Portfolio optimization
Up: Application Problems
Previous: Facility Location Problem (I)
The second facility
location problem we present has the following model:
min 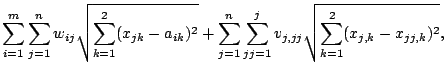 |
(3-6) |
where the definitions for 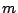 ,
, 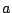 , and
, and 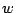 are the same as in the
previous case,
are the same as in the
previous case, 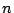 is the number of new facilities, and
is the number of new facilities, and 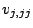 are the weights of the new-new connections. In a AMPL model,
emfl.mod in [16],
are the weights of the new-new connections. In a AMPL model,
emfl.mod in [16], 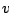 is defined as constant and
is defined as constant and 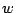 is
decided by the initial guess. The way of defining
is
decided by the initial guess. The way of defining 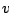 and
and 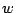 does
not seem realistic; however, they are still reasonable if one has
a good a initial guess. We now convert this problem to SOCP
format. First, we introduce
does
not seem realistic; however, they are still reasonable if one has
a good a initial guess. We now convert this problem to SOCP
format. First, we introduce
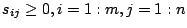 , and
, and
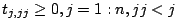 . Similarly, we need some additional
variables to replace
. Similarly, we need some additional
variables to replace
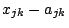 , and
, and
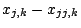 . By
rewriting
. By
rewriting 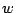 and
and 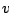 appropriately, we obtain the SOCP
formulation.
appropriately, we obtain the SOCP
formulation.
Example 3. To consider a simplified problem, we take an AMPL
model, emfl.mod, from [16]. In this model, the coordinates of
the existing facilities are generated randomly, the weight
associated with the new-new connections is fixed at 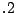 , and the
weight associated with the old-new connection is fixed by the
distance between the old facilities and the initial guesses. We
use the following four cases, (i)
, and the
weight associated with the old-new connection is fixed by the
distance between the old facilities and the initial guesses. We
use the following four cases, (i) 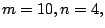 (ii)
(ii) 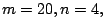 (iii)
(iii)
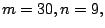 and (iv)
and (iv) 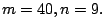



Next: Portfolio optimization
Up: Application Problems
Previous: Facility Location Problem (I)
Hans D. Mittelmann
2003-09-10
![]() , and the
weight associated with the old-new connection is fixed by the
distance between the old facilities and the initial guesses. We
use the following four cases, (i)
, and the
weight associated with the old-new connection is fixed by the
distance between the old facilities and the initial guesses. We
use the following four cases, (i) ![]() (ii)
(ii) ![]() (iii)
(iii)
![]() and (iv)
and (iv) ![]()