ZERO -- Zeros of Functions and Systems
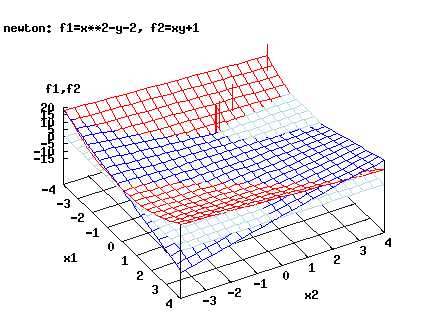
The following table shows performance of Newtons method for the problem f1=x**2-y-2=0 and f2=x*y+1=0 with initial guess -4,4
| x1 | x2 | f1 | f2 | ||inv(jacob)|| |
| -4.0000 | 4.0000 | 10.000 | -15.000 | .33333 |
| -2.4722 | 1.7778 | 2.3341 | -3.3951 | .48011 |
| -1.8176 | .87522 | .42851 | -.59082 | .60279 |
| -1.6346 | .63831 | .33506E-01 | -.43366E-01 | .65321 |
| -1.6182 | .61819 | .26912E-03 | -.33013E-03 | .65832 |
See also the picture. The solutions of the system occur where the three colors corresponding to the surfaces z=f1(x,y), z=f2(x,y) and z=0 (red, dark blue and light blue) meet. The iterates are represented by vertical bars.
Single Variable
| MANBIS | Package for Locating and Computing Efficiently Many Roots of a Function (C++) |
| f77-zero, C++ version, C version |
f is a function of one real variable (Brent-Decker method), using function values only, zerofinder , needs inclusion by change of sign on interval |
| SERVER | server routines for brent.shar (C) |
| polyzero | f is a polynomial of one complex variable and has real coefficients (least squares method, interactive/file input, f77/C) |
| MultRoot | f polynomial with real (inexact) coefficients, especially for multiple roots (Matlab) |
| companion C-version |
f polynomial with real coefficients, QR for eigenvalues of companion matrix |
| Aberth C-version |
f is a polynomial with complex coefficients |
| MPSolve | multiple precision, complex coefficients, f77/f90 |
| Muller C-version |
f is a general function of one complex variable |
| DFZERO | search for a zero in a given interval |
| RPOLY | find all zeroes of a real polynomial (Jenkins-Traub method) f90-version, C++-version, Javascript for RPOLY |
| Madsen | find all zeroes of a real polynomial, C++ version |
| CPOLY | find all zeroes of a complex polynomial (Jenkins-Traub method) f90-version, C-version, C++ version |
| RootFinder | find all zeroes of a complex polynomial (several methods, root refinement, Windows version, web-based version) |
| Polynomial Equation Solver | low degree algebraic solver and Jenkins-Traub, real and complex, various languages |
| RROOT | safely enclosing zeroes of a continuous function in an interval |
Multiple Variable
| MULTIPLICITY | Matlab software for computing multiplicity structure of nonlinear systems |
| RATIONAL | Four different rational solvers for sparse and dense LINEAR SYSTEMS using GMP, large test set (C) |
| KINSOL | part of the SUNDIALS suite for ODE/DAE (C, Fortran interface) |
| ALIAS | Solve systems of equations or inequalities with interval arithmetic (C++) |
| TRESNEI | Solve systems of equations or inequalities with least squares approach (Matlab) |
| box_zeros | f depends on one or more complex variables, zeros sought in box (based on TOMS666) |
| HYBRJ | f not too nonlinear, exact Jacobian (Powell's hybrid method) |
| HYBRD f90 version |
not too nonlinear, Powells hybrid method, finite difference Jacobian |
| DogLeg | Powell's dogleg method (Matlab) |
| csolve | Robust solver by C. Sims (Matlab) |
| STRSCNE | Trust region method for bound-constrained nonlinear systems (Matlab) |
| CoDoSol | Constrained dogleg method for nonlinear systems with simple bounds(Matlab) |
| CRBond's code | real/complex one/multidimensional rootfinders and LS solvers (C/C++) |
| Filtrane | part of Galahad, nonlinear constraint solver, filter method, f2003 |
| PITCON | f not too nonlinear, no good initial guess available, continuation method |
| LOCA | Library of continuation algorithms; uses bordering algorithm to permit very large dimensions; distributed memory parallel (C), part of Trilinos |
| Continuation Toolbox MatCont | Includes continuation of limit cycles and codim 1 bifurcations (Matlab) |
| AUTO | Another Matlab continuation toolbox (for dynamical systems) |
| SNES | part of PETSC , serial and MPI parallel versions |
| SALSA | Self-Adapting Large-scale Solver Architecture for linear and nonlinear systems |
| PEQN/PEQL | inexact Newton and inverse column update methods, for large/sparse problems |
| nnes | zeros sought in box: l<=x<=u, see also users' guide |
| DAFNE | differential equations approach with second order system inspired by mechanics |
| CHABIS | characteristic bisection method |
| BERTINI | Solving polynomial systems by homotopy continuation (C) |
| Bertini-Lab | Solving polynomial systems by homotopy continuation (Matlab) |
| EPSILON | Maple-based package for operations on polynomials including solving systems |
| HOMPACK | globally convergent continuation method for polynomial systems |
| HOMPACK90 | f90 version of HOMPACK |
| POLSYS_PLP | more sophisticated version of HOMPACK90 |
| TENSOLVE | A Software Package for Solving Systems of Nonlinear Equations and Nonlinear Least-squares Problems Using Tensor Methods f90 version |
| toms/795, PHCPACK | A general-purpose solver for polynomial systems by homotopy continuation |
| INTBIS | interval method, f77 |
(Constrained) minimization approach
Rootfinders based on Newtons method or its modification will run into considerable trouble when presented with a problem where singularities of the Jacobian occur. In this case the use of unconstrained or constrained minimization might help, since there exist minimization methods which are rather robust if the constraint gradients are linearly dependent. To use an unconstrained minimizer, choose e.g. f(x)=||F(X)||^2 (the Euclidean length squared) and minimize this with some code proposed in the unconstrained minimization section. To use a constrained minimizer, choose simply f==0 as an objective function and minimize this under the constraint F(x)=0. The following code works often successfully in this situation:
| LANCELOT A or LANCELOT B | augmented Lagrangian based method |