The Least Squares Problem
You will find two sections:
The unconstrained LSQ-Problem
The constrained LSQ-Problem
The unconstrained LSQ-Problem:
min f(x), f(x) = sumk K ( F(tk) - Phi(x,tk))2
n=dim(x), K=number of data points
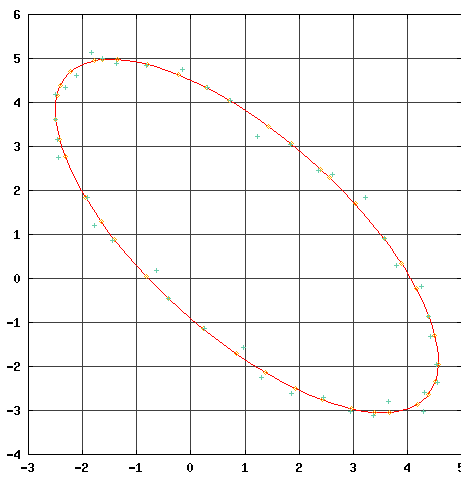
The picture shows you the problem of fitting an ellipse through 40 scattered data points in the plane in the sense of minimizing the sum of squared orthogonal distances, a so called orthogonal regression problem.
If f is quadratic in the unknowns we have a linear least squares problem (Phi is linear in the unkowns). This can be reduced in different ways to the solution of a system of linear equations. Since quite often the solution is very sensitive to roundoff errors, much care must be taken in doing this. The singular value decomposition is the ultimate tool here. Often use of the QR-(Householder)-decomposition suffices. We provide you with several software solutions for this.
f quadratic, n medium
| TRESNEI | trust-region Gauss-Newton method (Matlab) |
| netlib/lawson-hanson | solving the linear least squares problem using the singular value decomposition; this collection of routines and sample drivers includes in particular code for the solution of the nonnegative and the bound-constrained LS problems, of the problems arising in spline curve fitting, in least distance programming, as well as a demonstration of singular value analysis, f77&f90 |
| lapack/DGELSS C-version |
solves the linear least squares problem with several right hand sides, using the singular value decomposition. Matrix may be rank deficient. |
| toms/782 | Computing Rank-Revealing {QR} Factorizations of Dense Matrices |
| toms/853 | Modification of LAPACK's xGELSY; more efficient for low-rank matrices |
| UTV | Computing Rank-Revealing UTV decompositions of dense matrices |
| QRUP | QR factorization with row and column and rank-1 updates, Gram-Schmidt method |
| toms/686 | updating the QR factorization , Householder/Givens method |
Because of the bad fill in properties of orthogonal transformations the large scale linear least squares problem is much harder.
f quadratic, n large
| SuiteSparseQR | LS solution using a multithreaded multifrontal sparse QR factorization, C++ |
| SPARSE-QR | LS solution using a sparse QR decomposition, C/C++ |
| ARPACK | large sparse eigenvalue package, includes templates for SVD, parallel versions (f77, C++) |
| LMSVD | large sparse dominant SVD package (Matlab) |
| PROPACK | large sparse eigenvalue/SVD package (Matlab, f77) |
| netlib/svdpack | using different methods to compute leading singular pairs of sparse matrix, both f77 and C versions |
| LSQR and more | iterative solvers for large, sparse, possibly ill-conditioned linear least squares problems (f90,Matlab,Python,C++) |
| Meschach | numerical linear algebra in C, original source |
The nonlinear least squares problem occurs frequently in practice. If the data can be fitted well, then this is not much harder than a linear problem and special methods are quite successful.
f general, optimal f-value small (a "good fit"-problem)
| LMDER | The MINPACK Levenberg-Marquardt code, exact Jacobian, driver | |
| LMDIF | The MINPACK Levenberg-Marquardt code, Jacobian by finite differences,driver | |
| LMDIF_C | C-version of LMDIF (includes driver) | |
| lm_f90 | contains a f90-translation of LMDER/LMDIF above | |
| lmfit | Levenberg-Marquardt in Python | |
| lm_java | Levenberg-Marquardt in Java (needs JAMA) | |
| netlib/opt/varpro | separable problem, where Phi depends linearly on a part of the parameters (e.g. sum_i a_i*exp(b_i*t)). These can be treated in a special way, leaving a nonlinear problem of reduced dimension. | |
| dqed | self-contained version of Hanson&Krogh's netlib-code | |
| dqed_f90 | f90 version of Hanson&Krogh's netlib-code, related programs | |
| LMFnlsq | Fletcher's modification of Levenberg-Marquardt (Matlab) | |
| ELSUNC | Gauss-Newton method, analytic/numerical Jacobian, includes paper | |
| ELSUNC_f90 | f90-version and driver | |
| CERES | C++. new BSD-license, from Google |
If the optimal fit is "bad", then methods based on linearization of Phi are not successful. In this case either use a general minimizer or one of these (combination of Gauss-Newton with quasi-Newton for the second order derivatives of Phi):
f general, optimal f-value possibly large (bad fit)
| toms/573 | NL2SOL by Dennis, Gay, Welsch |
| port/n2f.f | newer version, needs other routines from port library, numerical gradients; n2g for exact gradients |
| port/nsf | explicit input of model functions, numerical gradients; nsg for exact gradients |
| f90-translations | of the above software |
| NL2SOL | another link to this and related software |
| LEVM | for complex functions, Windows executable, documentation |
| IMMOPTIBOX | Marquardt's and a hybrid method (Matlab) |
| LEVMAR | Unconstrained and linearly constrained Levenberg-Marquardt implementations (GPL, C/C++) |
| sparse Levenberg-Marquardt | sparse Levenberg-Marquardt implementations (GPL, C/C++) |
f from orthogonal regression
| netlib/odrpack/ | a large package for general orthogonal regression |
| odrpack95 | f95 version; bound constraints |
| gaussfit | Matlab version of code |
| STARPAC | legacy statistical Fortran package incl linear/nonlinear fitting |
| Nonlinear LS Curve Fitter | interactive Javascript-based tool |
f complex
| Complex Optimization Toolbox/ | Matlab package; incl tensor-valued residuals, bound constraint |
Applications
| SBA/ | spectral bundle adjustment for image reconstruction (C/C++) |
Total Least Squares
| VanHuffel | includes documentation, drivers f90 version |
f from autoregressive model
| ARfit | parameter estimation, checking, analyzing eigenmodes (Matlab) |
f from maximum-likelihood estimation, nonlinear model
| netlib/opt/nlr | nonlinear regression code by Bunch, Gay, and Welsch toms version |
| Fastfit | efficient maximum-likelihood estimation of various distribution, Matlab |
| MILES | efficient maximum-likelihood estimation of various distributions, Matlab |
| Probabilistic Modeling Toolkit for Matlab/Octave | Comprehensive toolbox for machine learning |
| S-estimator and more | Matlab software for robust regression |
| CMregr | computes constrained M-estimate, Matlab |
Regularization of discrete ill-posed problems
| Regularization Tools | Matlab package for analysis and solution of discrete ill-posed problems |
| Restore Tools | Object Oriented Matlab Package for Image Restoration |
Sparse Optimization, Compressive Sensing
| ASP, Sparse Optimization | Matlab routines for various sparse optimization problems |
| Compressive Sensing Software | Part of Rice U's CS resources (need to scroll way down) |
The constrained LSQ-Problem:
min f(x), f as above, subject to h(x)=0, g(x)>=0,
n=dim(x), m=dim(g), p=dim(h).
f is quadratic or general in x; bound constraints on x
| netlib/lawson-hanson | f quadratic, nonnegativity and bound constraints, f77&f90 |
| JavaNNLS | Java version |
| TSNNLS | Sparse nonnegative least squares, uses LAPACK, BLAS, TAUCS, LSQR (C) |
| ELSUNC | f general, Gauss-Newton method, analytic/numerical Jacobian, paper here |
| ELSUNC_f90 | f90-version and driver |
| port/n2fb | f general needs other routines from port library, numerical gradients, use n2gb for exact gradients |
| port/nsfb | explicit input of model functions, numerical gradients, use nsgb for exact gradients |
| BVLS | linear L1, L2, or Linf problems, active set method |
| BVLS.f90 | f90 version of BVLS by Alan Miller |
| BCLS | f quadratic. bound constraints, regularization term, only matrix multiplies needed, speedup with fast BLAS (C) |
| lsNTF | Computing nonnegative tensor factorizations; needs Matlab tensor toolbox (Matlab) |
f is quadratic in x; g,h linear (the linearly constrained least squares problem)
| LEVMAR | Unconstrained and linearly constrained Levenberg-Marquardt implementations (GPL, C/C++) |
| dqed | self-contained version of Hanson&Krogh's netlib-code, general linear constraints. |
| LSE | Computes LS solution of Ax~=b subject to Cx=d, C may be rank-deficient, Matlab |
| lapack/DGGLSE C-version |
linear equality constraints |
| toms/587 | hard/soft equality and inequality constraints |
| lapack/DGGGLM C-version |
general linear model (solving f=||y||, h=Ax+By-d, weighted LS for nonsingular square B) |
| UNIMOD | Unimodal, monotonic LS regression (Matlab) |
| L2WPMA | Weighted monotonic least squares |
nonlinear constraints, optimal f-value small
| SDLS | MATLAB code for solving three types of semidefinite constrained least squares problems |
| SDLS | a Matlab package for solving conic least-squares problems |
| ENLSIP | Gauss-Newton method, analytic/numerical Jacobians, also another NLSCON available, includes paper |
| gaussfit | own modeling language, documentation, testexamples, C |
| MILES | Least Squares with integer variables (Matlab) |