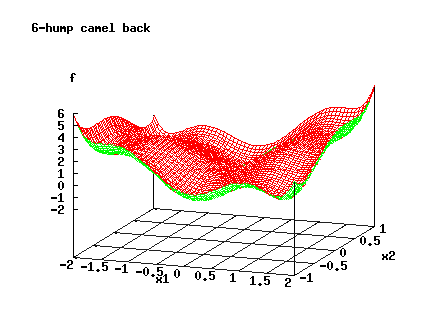
The occurrence of multiple extrema makes problem solving in nonlinear optimization even harder. Usually the user dreams of the global (best) minimizer, which might be difficult to obtain without supplying global information, which in turn is usually unavailable for a nontrivial case. The following picture shows the function

which has two global minima at (0.09,-0.71) and (-0.09,0.71) and four additional local minima.

The Unconstrained NLO-Problem:

min f(x), n=dim(x).

Global optimization is a difficult area, at least for larger n, since there is no easy algebraic characterization of global optimality. Most of the codes designed for minimization simply restrict themself to solve the equation grad(f(x))=0, which is only necessary of course. Methods using interval-arithmetic and branch&bound will in principle solve these problems, but the branch tree might become excessively large for difficult functions. Hence for higher dimensions and without special structure only stochastic or pseudostochastic methods will apply.
See however the books of Kearfott Rigorous Global Search: Continuous Problems Kluwer, Dordrecht 1996, Floudas Deterministic Global Optimization: Theory, Algorithms and Applications, Kluwer, Dordrecht 1999, and Hansen&Walster Global Optimization Using Interval Analysis, Marcel Dekker 2003. See A. Neumaier's paper on methods and software as well as J. Pinter's survey on available software and Sandia's survey on methods.
Mainly stochastic or heuristic search methods are available freely:

	ACRS	A derivative-free adaptively controlled random search algorithm for bound constrained problems
	INTERALG	Finds global minima and (all) solutions of nonlinear systems with specifiable accuracy (Python)
	PANMIN	Two stochastic methods, one MPI parallelized; use Merlin/MCL
	BTRK	f90-version of the derivative-free Boender-Timmer-Rinnoy Kan algorithm
	MHTB	Matlab Metaheuristics Toolbox plus many other codes
	PSwarm	Hybrid derivative-free solver (particle swarm & direct search), AMPL interface (C (also parallel), Matlab)
	MLOCPSOA	particle swarm paradigm, AMPL interface (C source, binaries)
	Global Optimization	meta-heuristic and hybrid methods, also constrained (Matlab)
	netlib/toms/667	method of Zirilli et al (stochastic differential equation approach)
	GANSO	several methods for global&nonsmooth problems, libraries for Win/Linux/Unix (C/C++)
	netlib/opt/simann	simulated annealing (f77)
	simannf90	f90-version from Alan Miller
	simann.m	Matlab version
	Anneal	C/C++/Ada/Forth implementations of SA
	JSimul	Java implementation of SA from Num Recipes
	ASA	C, adaptive simulated annealing, Matlab Interface
	CMA-ES	Evolution Strategy with Covariance Matrix Adaptation (Matlab)
	PGSL	A direct stochastic algorithm for global search incl constraints (C)
	Fortran-GA	genetic algorithm
	PGAPack	genetic algorithm, C, callable from Fortran
	PIKAIA	genetic algorithm; IDL, f90, parallel versions Excel version
	DGPF	Distributed Genetic Programming Framework. needs Eclipse for compile
	SIGOA	Simple Interface for Global Optimization Algorithms, Java source
	IGPE	Pseudo-deterministic method for the global estimation of parameters in dynamical systems (Matlab, GAMS)

These methods are simple to use, but require a high number of function evaluations if you desire acceptable final precision. Here are codes which determine the global minimum of a Lipschitz continuous function on a finite box:

	DIRECT (f77, Matlab)	using a bound for the Lipschitz constant of f and subdivision
	MCS	Huyer&Neumaier's Multilevel Coordinate search, local search by SQP, Matlab

The following codes fit a surrogate model to an expensive to evaluate function of few variables and analyze/minimize that:

	SPACE	global optimization through meta-modeling: fitting, cross -validation, prediction, minimization (C++)
	Spacemap	Optimization using Surrogate Models (Matlab)

The Constrained NLO-Problem:

min f(x) subject to h(x)=0, g(x)>=0,
n=dim(x), m=dim(g), p=dim(h).

Few codes are available but this is an area of current research and more links will be added. See also the book by Eldon Hansen, Global Optimization Using Interval Analysis, Dekker, New York, 1992.

For a good introduction into the theory see the book by Horst et al. For the state of the art until 1994, see the Horst&Pardalos handbook. A recent application-oriented overview is given in this book by Floudas.

	Black Box Opt	Black box functions and constraints, expensive evaluations, no derivatives needed (C, GPL)
	GloptiPoly	Polynomial objective and constraints, integer variables, needs SeDuMi (Matlab, GPL)
	SOSTOOLS	Matlab toolbox to solve sum of squares polynomial problems; needs SeDuMi and Matlab's symbolic toolbox (GPL)
	INTLAB	Matlab toolbox for self-validating algorithms
	DIRECT	version of DIRECT that handles general constraints using L1 penalty (Matlab)
	INTOPT_90	Interval software, f90, book, exhaustive search, automatic differentiation, bound and equality constraints, nonlinear systems, sources, binaries for SunOS and Win95, needs several local optimizers and linear algebra routines plus the author's interval package, superseded by GlobSol
	VerGO	C++, interval branch&bound, bound constraints, automatic differentiation, self-contained
	Genocop	various versions, including for nonlinear constraints (C)
	PGSL	A direct stochastic algorithm for global search incl constraints (C)
	FSA	simulated annealing, filter-set-based (Matlab)
	BARON	solves variety of global problems including discrete, free demo version from GAMS
	Maple GOT	toolbox containing both B&B and random methods

For more information on global optimization, see GLOBOPT