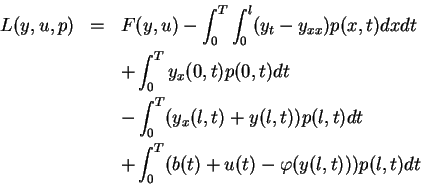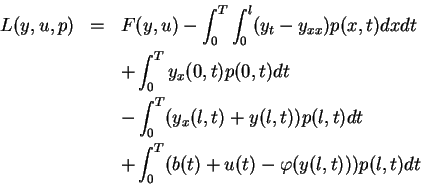

Next: Second Order Sufficient Conditions
Up: paper90
Previous: Parabolic and Elliptic Control
Known SSC Results for the Continuous Problems
No attempt will be made to quote all relevant results on optimality
conditions. In the case of problem (P) the following set of SSC is stated in
[1]. First, the Lagrange function
is defined with the Lagrange multiplier function 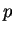 . Then the second
derivative of
. Then the second
derivative of 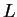 with respect to
with respect to 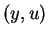 is called
is called 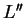 and is evaluated
at a point
and is evaluated
at a point
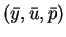 satisfying the first order optimality
conditions. The key requirement is the inequality
satisfying the first order optimality
conditions. The key requirement is the inequality
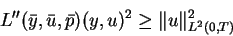 |
(3.1) |
which has to hold for all 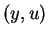 which satisfy the linearized (at
which satisfy the linearized (at
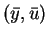 ) constraints. In the example considered in [1] and
below, the inequality even holds for all
) constraints. In the example considered in [1] and
below, the inequality even holds for all 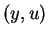 . Locally, then,
. Locally, then,
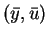 is a minimizer of problem (P).
is a minimizer of problem (P).
SSC have not been stated exactly for the two elliptic control problems (EB),
(ED) in the previous section, but a series of papers address special cases.
In [4], for example, a good overview of the literature is given
and the boundary control problem covered in much technical detail is nearly
identical to (EB) except for
On the other hand, a problem of type (ED) but with
and the tracking type objective function (2.3) is extensively analyzed in
[2]. Finally, the state-constrained case is addressed in
[5] for (EB) and in [20] for (P).


Next: Second Order Sufficient Conditions
Up: paper90
Previous: Parabolic and Elliptic Control
Hans D. Mittelmann
2001-06-17