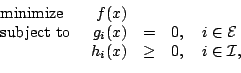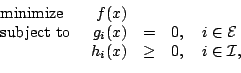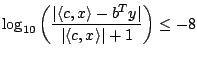

Next: BMPR
Up: The Codes
Previous: MOSEK
Authors: H. Y. Benson, Vanderbei
Version: 5.04, 8/2000;
Available: yes, from http://orfe.princeton.edu/ loqo/
Key paper: [27]
Features: NLP approach
Language, Input format: C; SDPA, Matlab, AMPL
Error computations: no
Solves: SOCP (SDP)
LOQO is a software package for solving general (smooth) nonlinear optimization problems of the form
where
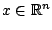 ,
,
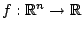 ,
,
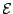 is the set of
equalities,
is the set of
equalities,
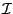 is the set of inequalities,
is the set of inequalities,
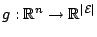 , and
, and
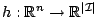 .
It implements an infeasible-primal-dual
path-following method and requires that the problem be smooth, that is
.
It implements an infeasible-primal-dual
path-following method and requires that the problem be smooth, that is 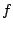 and
and
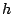 be twice differentiable, and
be twice differentiable, and 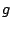 be an affine function.
Even though LOQO can handle nonconvex problems in general, it performs
better with convex problems, where
be an affine function.
Even though LOQO can handle nonconvex problems in general, it performs
better with convex problems, where 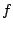 is convex,
is convex, 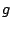 are affine,
and
are affine,
and 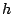 are concave functions.
are concave functions.
Stopping criteria
- LOQO can handle other types of nonlinear constraints in the problem.
- A weakness results from the use of the Cholesky factorization. LOQO
works best with a sparse problem, and it does not exploit the special
structure of an SOCP.
- Its SDP approach leads to dense problems.


Next: BMPR
Up: The Codes
Previous: MOSEK
Hans D. Mittelmann
2002-08-17