

Next: Appendix:Problem statistics and computational
Up: paper93
Previous: The Problems, Input formats,
-
- 1
- Andersen, E.D., Roos, C., Terlaky, T. (2000):
A primal-dual interior-point method
for conic quadratic optimization.
this volume
- 2
- Benson, S.J, Ye,, Y. (2001):
DSDP3: Dual scaling algorithm for general positive semidefinite
programming.
Preprint ANL/MCS-P851-1000, Argonne National Labs
- 3
- Borchers, B. (1999):
CSDP, A C library for semidefinite programming.
Optimization Methods and Software 11, 613-623
- 4
- Burer, S., Monteiro, R.D.C. (2001):
A nonlinear programming algorithm for solving
semidefinite programs via low-rank factorization.
this volume
- 5
- Burer, S., Monteiro, R.D.C., Zhang, Y. (2001):
Solving a class of semidefinite programs via nonlinear programming.
Computational and Applied Mathematics, Rice University, Houston,
Revised December 1999 and May 2001, submitted to Mathematical Programming
- 6
- Burer, S., Monteiro, R.D.C., Zhang, Y. (2001):
A computational study of a gradient-based log-barrier algorithm
for a class of large-scale SDPs.
this volume
- 7
- Burer, S., Monteiro, R.D.C., Zhang, Y. (2001):
Interior-point algorithms for semidefinite programming based on a
nonlinear formulation.
Department of Industrial and Systems Engineering,
Georgia Institute of Technology, Atlanta,
submitted to Computational Optimization and Applications
- 8
- DIMACS 7th Challenge website,
http://dimacs.rutgers.edu/Challenges/Seventh/
- 9
-
Fujisawa, K., Fukuda, M., Kojima, M., Nakata, K (1999):
Numerical evaluation of SDPA (SemiDefinite Programming
Algorithm).
High Performance Optimization, Kluwer Academic Publishers,
267-301
- 10
-
Fujisawa, K., Kojima, M., Nakata, K (1997):
Exploiting sparsity in primal-dual interior-point
methods for semidefinite programming.
Mathematical Programming 79, 235-253
- 11
-
Fujisawa, K., Kojima, M., Nakata, K (2000):
SDPA (Semidefinite Programming Algorithm) - User's Manual.
Technical Report B-308, Tokyo Institute of Technology,
http://is-mj.archi.kyoto-u.ac.jp/~ fujisawa/sdpa_doc.pdf
- 12
-
Helmberg, C. (2000):
SBmethod -- a C++ implementation of the spectral bundle
method.
Manual to Version 1.1, ZIB-Report ZR 00-35, Konrad-Zuse-Zentrum für
Informationstechnik Berlin,
http://www.mathematik.uni-kl.de/ helmberg/SBmethod/
- 13
-
Helmberg, C., Kiwiel, K.C. (1999):
A spectral bundle method with bounds.
ZIB Preprint SC-99-37, Konrad-Zuse-Zentrum für Informationstechnik
Berlin, to appear in Mathematical Programming
- 14
-
Helmberg, C., Rendl, F., Vanderbei, R.J., Wolkowicz, H. (1996):
An interior-point method for semidefinite programming,
SIAM Journal on Optimization 6, 342-361
- 15
-
Helmberg, C., Rendl, F. (2000):
A spectral bundle method for semidefinite programming.
SIAM Journal on Optimization 10, 673-696
- 16
-
Kiwiel, K.C. (1990):
Proximity control in bundle methods for convex nondifferentiable
minimization.
Mathematical Programming 46, 105-122
- 17
- Kojima, M., Shindoh, S., Hara, S. (1997):
Interior-point methods for the monotone semidefinite
linear complementarity problems.
SIAM Journal on Optimization 7, 86-125
- 18
- Mittelmann, H.D. (2002):
Decision Tree for Optimization Software.
http://plato.la.asu.edu/guide.html
- 19
- Mittelmann, H.D. (2002):
Benchmarks for Optimization Software.
http://plato.la.asu.edu/bench.html
- 20
- Andersen, E. (2002):
MOSEK User's Guide: The MPS file format.
http://www.mosek.com/download/doc/html/2/tools/manual/node15.html
- 21
- NEOS Server for Optimization.
http://www-neos.mcs.anl.gov/neos/
- 22
- Rendl, F., Sotirov, R., Wolkowicz, H. (2001):
Exploiting sparsity in interior point methods:
Applications to SDP and QAP. Department of Combinatorics and
Optimization, University of Waterloo,
Waterloo, Canada, in progress
- 23
-
Stewart, D.E., Leyk, Z. (1994):
Meschach: Matrix Computation in C.
Proceedings of the Center for Mathematics and Its Applications,
The Australian National University, Volume 32
- 24
-
Sturm, J.F. (1999):
Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones.
Optimization Methods and Software 11, 625-653
- 25
-
Sturm, J.F. (2000):
Central region method,
in High Performance Optimization, J.B.G. Frenk and C. Roos and T. Terlaky and S. Zhang (eds.), Kluwer Academic Publishers, 157-194
- 26
- Tütüncü, R.H., Toh, K.C., Todd (2002):
Solving semidefinite-quadratic-linear programs using SDPT3.
this volume
- 27
-
Benson, H.Y., Vanderbei, R.J. (2002):
Solving Problems with Semidefinite and Related Constraints Using
Interior-Point Methods for Nonlinear Programming.
this volume
- 28
-
Ye, Y., Todd, M.J., Mizuno, S. (1994):
An
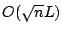 -iteration homogeneous and self-dual linear programming algorithm.
Mathematics of Operations Research 19, 53-67
-iteration homogeneous and self-dual linear programming algorithm.
Mathematics of Operations Research 19, 53-67
Hans D. Mittelmann
2002-08-17