Example 4

In this and the following examples we choose Neumann boundary conditions. We modify Example 3 and consider the problem:

$$\begin{eqnarray*} \hspace*{-11mm} \begin{array}{lll} \mbox{on} \;\;\Omega \,: & ... ...) = 0, &\; u_d(x) \equiv 0 \,, \; \alpha = 0.001 . \end{array}\end{eqnarray*}$$

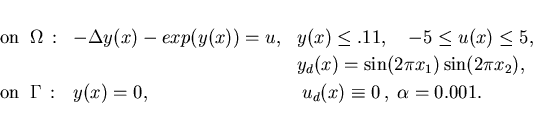
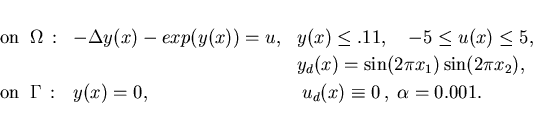
The adjoint equation agrees with (4.4) except that we obtain a Neumann boundary condition

$$\partial_{\nu} \bar{q}(x) + \bar{q}(x) = 0 \qquad \mbox{on} \;\; \Gamma \,. \quad$$ (4.6)

The minimum condition (2.21) gives the projection (4.5) with $\,[u_1,u_2] = [-8,9]\,$. Figure 7 shows the optimal control while Figure 8 depicts the optimal state and associated adjoint variable. The reader may verify that the control rule (4.5) is satisfied.

Figure 7: Example 4, $\,\alpha =0.001$ : Optimal control.

Figure 8: Example 4, $\,\alpha =0.001$ : Optimal state and adjoint variable

Table 4: Detailed information on solution of Example 4

N+1	it	AMPL	LOQO	Acc	$F(\bar{y},\bar{u})$	$y(.5,.5)$	$u(.5,.5)$
50	26	.2	110	8	.0773888	-.011311	-1.688123
100	23	1	1325	8	.0780638	-.009160	-1.620104
200	25	4	43640	8	.0784259	-.008243	-1.588789

This example will also be used to illustrate the numerical process in more detail. The platform is a 450 MHz Pentium-II PC with Linux-2.2.12. Table 4 summarizes the data: size of grid, number of iterations of LOQO, times in seconds for the AMPL compilation and the solution by LOQO, the accuracy as the number of correct significant digits in the discrete objective function value only. The primal-dual approach yields upper and lower bounds for this value and thus permits such a statement. In all the examples solved this accuracy measure was at least 8 showing that LOQO had converged satisfactorily. However, from the accuracy of the objective function value no similar accuracy of the computed solution components may in general be inferred. In fact, for the discretizations used they may be expected to have at most a few correct digits. Finally, we list the objective function value and the value in the center of the domain of both the state and the control variable. These values show that only a moderate accuracy may be expected.

Table 5: Comparison of different solvers on Example 4

N+1	LANCELOT	LOQO	MINOS	SNOPT
50	4.4	1	5.8	71
100	16	1	3.1	88
200	-	1	inf	inf

We compare LOQO and other solvers with AMPL interface available to us in Table 5; links to all codes in [24]. Given are CPU times in seconds on the same platform used above, but scaled by LOQO's time. MINOS and SNOPT report the largest problem as infeasible while LANCELOT needs excessive compute time. Both SNOPT and MINOS are designed for problems with a moderate number of degrees of freedom, about $2000$ and thus should not be expected to be able to handle the larger instances. See, however, the results for Example 5 which has a very small number of degrees of freedom, understood here as the difference between the number of variables and the number of active constraints. All solvers were given the same AMPL file and AMPL initializes variables with zero if no explicit initialization is made. In summary one can say that for $N+1=100$ the computing times for LOQO are acceptable and that the computed solutions, both function values and variables, appear to be in error by a few units in the third significant digit.

Figure 9: Example 5, $\,\alpha =0$ : Optimal control and state.

Figure 10: Example 5, $\,\alpha =0$ : Adjoint variable and switching locus $\bar{q}(x)=0$.