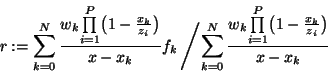 |
(4) |
It should be noted that it is not possible that a pole zi thereby comes to lie in the interval [-1,1]: the corresponding r could never be a best approximation to the continuous f. In particular, no zi can be 0.
The existence of an optimum is easily seen.
For that purpose, write r as
The unicity question is more involved.
The constant function example ![]() (and, more generally,
every polynomial of degree less or equal to N-P) shows
that there are
(and, more generally,
every polynomial of degree less or equal to N-P) shows
that there are
![]() for which no pole can be attached to p [4]:
every set of numbers replacing the wk in (1) results in
for which no pole can be attached to p [4]:
every set of numbers replacing the wk in (1) results in ![]() (which
appears only reasonable from an approximation point of view).
In practical computations, such a large connected set of optimal points
manifests itself in the
optimization routine going around without direction.
(which
appears only reasonable from an approximation point of view).
In practical computations, such a large connected set of optimal points
manifests itself in the
optimization routine going around without direction.
Unicity is warranted if the optimization yields
![]() ,
i.e., if r=fon [-1,1]. Indeed, when two analytic functions r1, r2 agree on an interval
I, then r1 = r2 on every domain of analyticity containing I, by the
fundamental lemma on analytic continuation [13, p. 150]. Therefore
,
i.e., if r=fon [-1,1]. Indeed, when two analytic functions r1, r2 agree on an interval
I, then r1 = r2 on every domain of analyticity containing I, by the
fundamental lemma on analytic continuation [13, p. 150]. Therefore
![]() if and only if
if and only if
![]() on [-1,1].
Numerically, however, the unicity shows up only if P is not chosen larger than the
actual number of poles of f, for otherwise the condition of the problem is so good
that many combinations of P poles yield
on [-1,1].
Numerically, however, the unicity shows up only if P is not chosen larger than the
actual number of poles of f, for otherwise the condition of the problem is so good
that many combinations of P poles yield
![]() ,
,
![]() unit-roundoff error of the machine.
unit-roundoff error of the machine.
The unicity question can also be narrowed to an interesting one,
to which we do not have the answer.
It is obvious from the above construction that nonvanishing of the
numerator at zi is
a sufficient condition for r to have a pole there. We have checked
this condition in its equivalent form [4]
We want to point to another representation of (5).
Indeed,
![]() is the leading coefficient
of the polynomial interpolating a function g between the xk's,
and this coefficient
is the divided difference
of g with respect to all xk's [2]. Condition (5) can therefore
be written as
is the leading coefficient
of the polynomial interpolating a function g between the xk's,
and this coefficient
is the divided difference
of g with respect to all xk's [2]. Condition (5) can therefore
be written as
A nice property of the suggested interpolation deserves special notice:
the approximation error
cannot increase with the number of poles, this in sharp contrast with
classical rational
interpolation. Indeed,
as a new unknown, say zP, is
added to the set of variables,
![]() ,
the optimal
value of the latter is a
feasible vector for the higher dimensional optimization--simply set
,
the optimal
value of the latter is a
feasible vector for the higher dimensional optimization--simply set
![]() in (4).
In particular, attaching poles to the
interpolating polynomial can never worsen the quality of the approximation.
in (4).
In particular, attaching poles to the
interpolating polynomial can never worsen the quality of the approximation.