

Next: Conclusions
Up: No Title
Previous: Steady Progressing Wave Solutions
We performed numerical simulations of these models
using the method of lines. In this, we model the integrodifferential
equation using a set of 200 ordinary differential equations.
In the cases presented here, the connection polarities
are taken to be
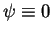 ,
the components of
f and of K are cosines, and we solved the system
,
the components of
f and of K are cosines, and we solved the system
for
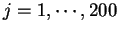 .
.
A series of computations was done for the single
and double layer cases. In the two examples presented
here, the initial data had the form
for
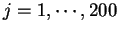 ,
where Rj is a
uniformly distributed random variable
having
,
where Rj is a
uniformly distributed random variable
having
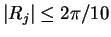 .
.
We calculate the solutions to time 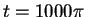 using an adaptive step
Runge-Kutta scheme of orders 7 and 8 [12], and by that time
the solution had achieved the form
using an adaptive step
Runge-Kutta scheme of orders 7 and 8 [12], and by that time
the solution had achieved the form
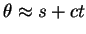 and the wave speed (c) is estimated by evaluating
and the wave speed (c) is estimated by evaluating
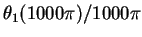 .
.
The results of the single layer simulation are shown in
the Figure 1. In this,
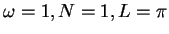 and the predicted wave speed is
and the predicted wave speed is 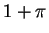 .
In Figure 2
we plot the numerical error, which is deviation of
our calculated solution from the theoretical solution
derived above
.
In Figure 2
we plot the numerical error, which is deviation of
our calculated solution from the theoretical solution
derived above
at
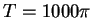 .
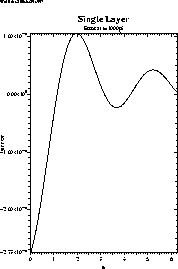
We see there that the error is
O(10-6)for this simulation.
.
We see there that the error is
O(10-6)for this simulation.
Figure:
Initial data (top) and
calculated solution
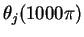 (bottom).
In this case,
(bottom).
In this case,
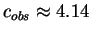 and
and
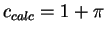 .
.
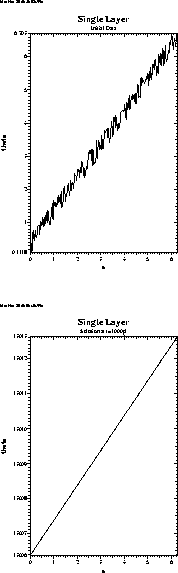 |
Figure 2:
Error of our computer simulation of the single layer model
shown in Figure 1.
 |
In the case of two layers, we take similar initial data
for each of the two layers as described above, but we take
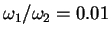 .
The results are shown in Figure 3
This simulation demonstrates that a striated structure can support
different wave speeds.
.
The results are shown in Figure 3
This simulation demonstrates that a striated structure can support
different wave speeds.
Figure:
Plotted here are
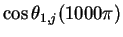 (top)
and
(top)
and
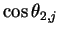 (bottom). The estimated wave speeds
in these cases are
c1 = 5.01 and
c2 =0.264.
(bottom). The estimated wave speeds
in these cases are
c1 = 5.01 and
c2 =0.264.
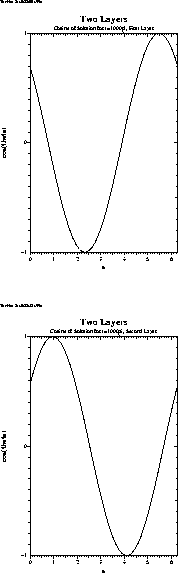 |


Next: Conclusions
Up: No Title
Previous: Steady Progressing Wave Solutions
Hans Mittelmann
2000-04-04
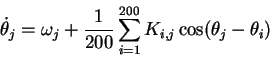
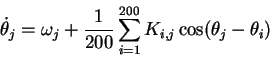
![]() using an adaptive step
Runge-Kutta scheme of orders 7 and 8 [12], and by that time
the solution had achieved the form
using an adaptive step
Runge-Kutta scheme of orders 7 and 8 [12], and by that time
the solution had achieved the form
![]() and the wave speed (c) is estimated by evaluating
and the wave speed (c) is estimated by evaluating
![]() .
.
![]() and the predicted wave speed is
and the predicted wave speed is ![]() .
In Figure 2
we plot the numerical error, which is deviation of
our calculated solution from the theoretical solution
derived above
.
In Figure 2
we plot the numerical error, which is deviation of
our calculated solution from the theoretical solution
derived above
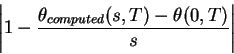
![]() .
The results are shown in Figure 3
This simulation demonstrates that a striated structure can support
different wave speeds.
.
The results are shown in Figure 3
This simulation demonstrates that a striated structure can support
different wave speeds.
