Computing Errors

Suppose that we are given approximate optimal solutions of ($SQLP-P$) and ($SQLP-D$), respectively. To compute how far they are from an exact solution pair, we define a norm on $X$, and a minimum eigenvalue w.r.t. the cone $K$. Precisely, if $x \in X$, then

$$\vert\!\vert x \vert\!\vert = \sum_{j=1}^{n_s} \vert\!\vert x^s_j... ...vert\!\vert x^q_k \vert\!\vert _2 \, + \, \vert\!\vert x^\ell \vert\!\vert _2,$$

where for a matrix $a$, $\vert\!\vert a \vert\!\vert _F$ is the Frobenius norm of $a$. Also,

$$\lambda_{\min, K}(x) = \min \, \biggl\{ \min_{j=1, \dots, n_s} \l... ...min_{k=1, \dots, n_q} \lambda_{\min,q}(x^q_k), \, \min_{h} x^\ell_h \biggr\}$$

where

• for a symmetric matrix $a$, $\lambda_{\min}(a)$ is the usual smallest eigenvalue of $a$.
• for a vector $a$, $\lambda_{\min,q}(a) = a_1 - \vert\!\vert a_{2:k} \vert\!\vert _2$.

Also, we denote by $\vert\!\vert a \vert\!\vert _1$ the absolute value of the largest component of $a$, for an arbitrary $a \in X$.

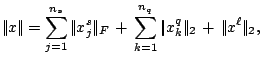
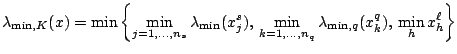
Then, for approximate optimal solutions $x$ of ($SQLP-P$) and $(y,z)$ of ($SQLP-D$), we define

$${\rm err }_1(x,y,z) = \frac{\vert\!\vert \mathcal{A}x - b \vert\!\vert}{1+ \vert\!\vert b \vert\!\vert _1}$$

$${\rm err }_2(x,y,z) = \max \biggl\{ 0, \frac{-\lambda_{\min,K}(x)}{1+ \vert\!\vert b \vert\!\vert _1} \biggr\}$$

$${\rm err }_3(x,y,z) = \frac{\vert\!\vert \mathcal{A}^* y + z - c \vert\!\vert}{1 + \vert\!\vert c \vert\!\vert _1}$$

$${\rm err }_4(x,y,z) = \max \biggl\{ 0, \frac{-\lambda_{\min,K}(z)}{1+ \vert\!\vert c \vert\!\vert _1} \biggr\}$$

$${\rm err }_5(x,y,z) = \frac{\langle c, x \rangle - b^T y }{1+ \vert \langle c, x \rangle \vert + \vert b^T y \vert}$$

Furthermore, when $x$ and $z$ are both in $K$, that is ${\rm err }_2(x,y,z) = {\rm err }_4(x,y,z) = 0$, we also define

$${\rm err }_6(x,y,z) = \frac{\langle x, z \rangle }{1+ \vert \langle c, x \rangle \vert + \vert b^T y \vert}$$

A few remarks are in order.

• If $x$ and $z$ are both feasible, then in exact arithmetic ${\rm err }_5(x,y,z) = {\rm err }_6(x,y,z)$.
• As $x$ and $z$ are approximate optimal solutions only, we may have ${\rm err }_5(x,y,z) < 0$. It is possible that all other error measures being the same, if ${\rm err }_5(x,y,z) = - \delta$ with $\delta >0$ corresponds to a solution that is ``worse'', than as if ${\rm err }_5(x,y,z)$ was $\delta$. Thus, we decided to report ${\rm err }_5(x,y,z)$, not merely the maximum of ${\rm err }_5(x,y,z)$ and 0 (as it is done in several papers), so as not to suppress any information.
• Several codes do not explicitly maintain $z$; in this case, one should set
  $$z = c - \mathcal{A}^* y$$
  Of course, then ${\rm err }_3(x,y,z)$ will be zero (depending on the accuracy achieved by the computer).

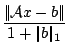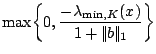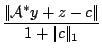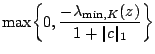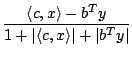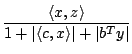In the error tables below ${\rm err }_1$ and ${\rm err }_5$ are always listed. ${\rm err }_2$ is only given when nonzero and ${\rm err }_6$ only when in the digits shown different from ${\rm err }_5$. ${\rm err }_6$ is not available for SDPA.

From the time the benchmark problems for the Challenge were published until the time the papers for this volume were due we have performed an evaluation of the codes on all the benchmark problems each code could solve. In most cases we had the latest version of the codes which the authors themselves used and on which their contributions to the volume are based. An exception is the code SDPA. Its authors are reporting about work done after release of their software and which is not yet available in coded form. The codes BMPR and BMZ were released once and not updated. All remaining codes were updated at least once, several at the time of the workshop or thereafter. Substantial changes were done with DSDP which evolved from a special code for discrete graph problems to a general purpose SDP solver accepting also standard sparse SDPA input format. Further quite remarkable improvements were applied to SDPT3, BUNDLE, and CSDP.

These benchmark results are meant to yield a rough overview of how the tested codes performed on the same, standard platform, a Sun Ultra 60 with Solaris 8, 2 GB of memory, and a 450 MHz processor. Paging was avoided. In the following section first basic information is given on each participating code. Then, as provided by the authors, a short description follows of the code itself, the stopping criteria used, and the perceived strengths and weaknesses. In the third section the test problems are listed followed by some remarks regarding the performance of the codes. Appended are tables with problem statistics and the benchmark results.