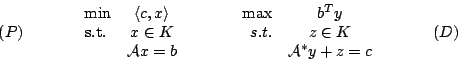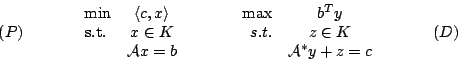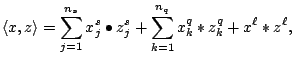

Next: Computing Errors
Up: Introduction
Previous: Introduction
The primal and dual pair of conic optimization problems over a self-dual cone are defined as
where
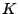 is a closed, convex cone in a euclidean space
is a closed, convex cone in a euclidean space 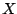 .
.
-
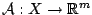 is a linear operator, and
is a linear operator, and
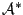 is its adjoint.
is its adjoint.
-
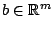 , and
, and 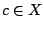 .
.
In the case of a semidefinite-quadratic-linear program these
are defined as follows:
Thus (P) and (D) become
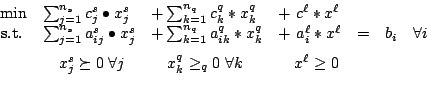 |
( ) ) |
and
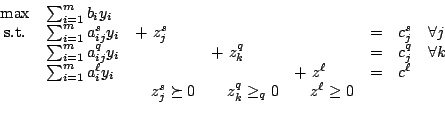 |
(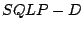 ) ) |
Thus the feasible set is a product of semidefinite,
quadratic and nonnegative orthant cones, intersected with an affine subspace.
It is possible that one or more of the three parts of the problem is
absent, i.e., any of 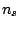 ,
, 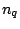 , or the length of
, or the length of 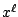 may be zero.
may be zero.
The rotated quadratic cone is defined as
It is simply a rotation of the usual quadratic cone, but for the purpose of modeling quadratic
inequalities, it is more convenient to use, thus several participating codes support this cone.


Next: Computing Errors
Up: Introduction
Previous: Introduction
Hans D. Mittelmann
2002-08-17