

Next: The Problems, Input formats,
Up: The Codes
Previous: BMZ
Authors: Helmberg [Kiwiel, Rendl]
Version: SBmethod1.1.1, 11/2000;
Available: yes, from http://www.mathematik.uni-kl.de/ helmberg/SBmethod/
Key papers: [12,13,15,16]
Features: eigenvalue optimization
Language, Input format: C++; graph
Error computations: norm of subgradient only
Solves: maxcut, FAP, bisection, theta
SBmethod, Version 1.1.1, is an implementation of the spectral bundle
method [15,13] for eigenvalue optimization
problems of the form
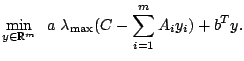 |
(1) |
The design variables 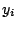 may be sign constrained,
may be sign constrained, 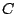 and the
and the 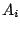 are given
real symmetric matrices,
are given
real symmetric matrices,
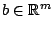 allows to specify a linear cost
term, and
allows to specify a linear cost
term, and 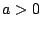 is a constant multiplier for the maximum eigenvalue function
is a constant multiplier for the maximum eigenvalue function
 . The code is intended for large scale problems and
allows to exploit structural properties of the matrices such as sparsity and
low rank structure (see the manual [12]). Problem
(1) is equivalent to the dual of semidefinite programs
. The code is intended for large scale problems and
allows to exploit structural properties of the matrices such as sparsity and
low rank structure (see the manual [12]). Problem
(1) is equivalent to the dual of semidefinite programs
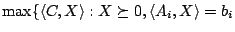 for
for
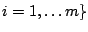 with constant trace,
with constant trace,
 .
.
The code is a subgradient method in the style of the proximal bundle method of
[16]. Function values and subgradients of the nonsmooth convex
function
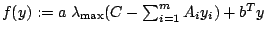 are
determined via computing the maximum eigenvalue and a corresponding eigenvector
by the Lanczos method. Starting from a given point
are
determined via computing the maximum eigenvalue and a corresponding eigenvector
by the Lanczos method. Starting from a given point
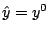 , the algorithm
generates the next candidate
, the algorithm
generates the next candidate
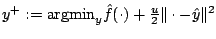 , where
, where 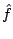 is an accumulated semidefinite cutting model minorizing
is an accumulated semidefinite cutting model minorizing 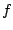 and the dynamically updated weight
and the dynamically updated weight 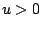 keeps
keeps 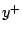 near
near 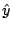 . A descent step
. A descent step
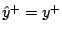 occurs if
occurs if
![$ f(\hat y)-f(y^+)\ge\kappa[f(\hat y)-\hat f(y^+)]$](img153.gif) , where
, where
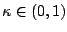 . Otherwise a null step
. Otherwise a null step
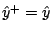 is made but
the next model is improved with the new eigenvector computed at
is made but
the next model is improved with the new eigenvector computed at 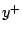 .
.
The algorithm stops, when
 for a given termination
parameter
for a given termination
parameter
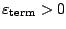 which is
which is 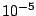 by default.
by default.
- The code never factorizes the matrix
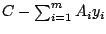 but uses matrix
vector multiplications exclusively. Thus, there is no danger of increasing
memory requirements or computational work by additional fill-in.
but uses matrix
vector multiplications exclusively. Thus, there is no danger of increasing
memory requirements or computational work by additional fill-in.
- Experimentally,
the method seems to exhibit fast convergence if the semidefinite subcone that
is used to generate the semidefinite cutting surface model, spans the optimal
solution of the corresponding primal problem.
- If the subcone, however, is
too small, the typical tailing off effect of subgradient methods is observed.


Next: The Problems, Input formats,
Up: The Codes
Previous: BMZ
Hans D. Mittelmann
2002-08-17
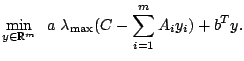
![]() are
determined via computing the maximum eigenvalue and a corresponding eigenvector
by the Lanczos method. Starting from a given point
are
determined via computing the maximum eigenvalue and a corresponding eigenvector
by the Lanczos method. Starting from a given point
![]() , the algorithm
generates the next candidate
, the algorithm
generates the next candidate
![]() , where
, where ![]() is an accumulated semidefinite cutting model minorizing
is an accumulated semidefinite cutting model minorizing ![]() and the dynamically updated weight
and the dynamically updated weight ![]() keeps
keeps ![]() near
near ![]() . A descent step
. A descent step
![]() occurs if
occurs if
![]() , where
, where
![]() . Otherwise a null step
. Otherwise a null step
![]() is made but
the next model is improved with the new eigenvector computed at
is made but
the next model is improved with the new eigenvector computed at ![]() .
.
![]() for a given termination
parameter
for a given termination
parameter
![]() which is
which is ![]() by default.
by default.