Abstract:

Adaptive time-stepping based on linear digital control theory has several advantages: the algorithms can be analyzed in terms of stability and adaptivity, and they can be designed to produce smoother stepsize sequences resulting in significantly improved regularity and computational stability. 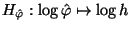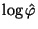Here we extend this approach by viewing the closed loop transfer map $H_{\hat\varphi}:\log\hat\varphi\mapsto\log h$ as a digital filter, processing the signal $\log\hat\varphi$ (the principal error function) in the frequency domain, in order to produce a smooth stepsize sequence $\log h$. 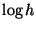General controllers of up to third order dynamics are considered for adaptive time-stepping in the asymptotic stepsize-error regime. The theory, which covers all previously considered control structures, offers new possibilities to use different design objectives and construct stepsize selection algorithms for different purposes, such as higher order of adaptivity (for smooth ODE problems) or a stronger ability to suppress high-frequency error components (non-smooth problems, stochastic ODEs). The controllers are tested in simulations to verify their ability to produce stepsize sequences resulting in improved regularity and computational stability.