Constraints:
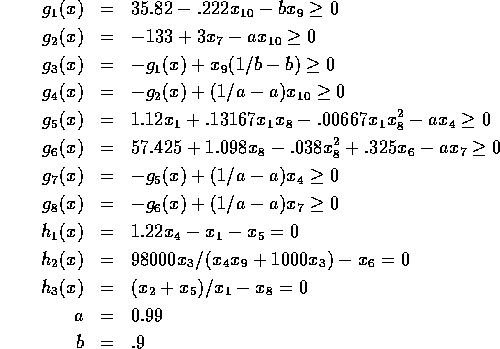
Solution: Primal
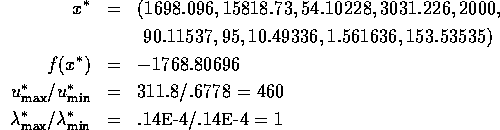

This problem comes originally from Bracken & McCormick. It is
listet with 118 others in W. Hock, K. Schittkowski:
Test Examples for Nonlinear Programming Codes.
Lecture Notes in Econ and Math. Syst. 187
The mathematical description of the problem is shown first:
Problem 114 (alkylation process)
Number of variables: n=10
Objective Function:
![]()
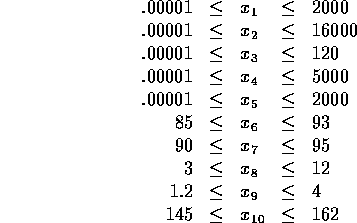
Constraints:
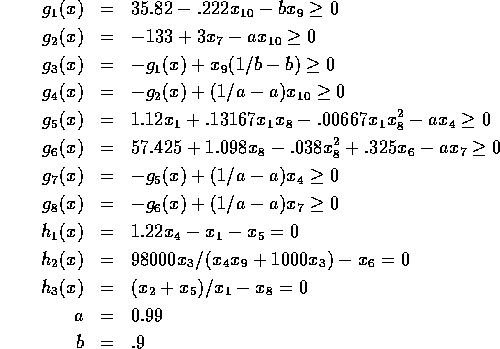

Solution: Primal ![]() , dual
, dual ![]() , eigenvalues of reduced Hessina
, eigenvalues of reduced Hessina ![]() .
.
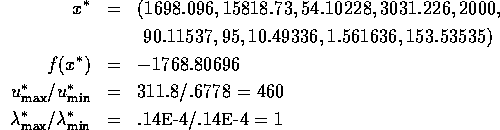

And this is the problem description in AMPL:
param n := 10;
set I := 1..n;
param lb{I};
param ub{i in I} > lb[i];
param x0{I};
param a := .99;
param b := .9;
var x{i in I} >= lb[i] <= ub[i] := x0[i];
minimize f: 5.04*x[1] + .035*x[2] + 10*x[3] + 3.36*x[5] - .063*x[4]*x[7];
var G1 = 35.82 - .222*x[10] - b*x[9];
var G2 = -133 + 3*x[7] - a*x[10];
var G5 = 1.12*x[1] + .13167*x[1]*x[8] - .00667*x[1]*x[8]^2 - a*x[4];
var G6 = 57.425 + 1.098*x[8] - .038*x[8]^2 + .325*x[6] - a*x[7];
s.t. g1: G1 >= 0;
s.t. g2: G2 >= 0;
s.t. g3: -G1 + x[9]*(1/b - b) >= 0;
s.t. g4: -G2 + (1/a - a)*x[10] >= 0;
s.t. g5: G5 >= 0;
s.t. g6: G6 >= 0;
s.t. g7: -G5 + (1/a - a)*x[4] >= 0;
s.t. g8: -G6 + (1/a - a)*x[7] >= 0;
s.t. g9: 1.22*x[4] - x[1] - x[5] = 0;
s.t. g10: 98000*x[3]/(x[4]*x[9] + 1000*x[3]) - x[6] = 0;
s.t. g11: (x[2] + x[5])/x[1] - x[8] = 0;
data;
param : lb ub x0 :=
1 .00001 2000 1745
2 .00001 16000 12000
3 .00001 120 110
4 .00001 5000 3048
5 .00001 2000 1974
6 85 93 89.2
7 90 95 92.8
8 3 12 8
9 1.2 4 3.6
10 145 162 145
;
Now the coding of this problem in C follows in the format required by P. Spellucci'c code donlp2 :
/* *************************************************************** */
/* objective function */
/* *************************************************************** */
void ef(DOUBLE x[],DOUBLE *fx) {
*fx = 5.04e0*x[1]+.035e0*x[2]+10.e0*x[3]+3.36e0*x[5]-.063e0*x[4]*x[7];
return;
}
/* *************************************************************** */
/* gradient of objective function */
/* *************************************************************** */
void egradf(DOUBLE x[],DOUBLE gradf[]) {
static INTEGER j;
static DOUBLE a[11] = {0.,/* not used : index 0 */
5.04e0,0.035e0,10.e0,0.e0,3.36e0,
0.e0 ,0.e0 , 0.e0,0.e0,0.e0};
for (j = 1 ; j <= 10 ; j++) {
gradf[j] = a[j];
}
gradf[4] = -0.063e0*x[7];
gradf[7] = -0.063e0*x[4];
return;
}
/* ************************************************************** */
/* compute the i-th equality constaint, value is hxi */
/* *****************************************************************/
void eh(INTEGER i,DOUBLE x[],DOUBLE *hxi) {
switch (i) {
case 1:
*hxi = 1.22e0*x[4]-x[1]-x[5];
break;
case 2:
*hxi = 9.8e4*x[3]/(x[4]*x[9]+1.e3*x[3])-x[6];
break;
case 3:
*hxi = (x[2]+x[5])/x[1]-x[8];
break;
}
return;
}
/* *****************************************************************/
/* compute the gradient of the i-th equality constraint */
/* *****************************************************************/
void egradh(INTEGER i,DOUBLE x[],DOUBLE gradhi[]) {
static INTEGER j;
static DOUBLE t,t1;
for (j = 1 ; j <= 10 ; j++) {
gradhi[j] = 0.e0;
}
switch (i) {
case 1:
gradhi[1] = -1.e0;
gradhi[4] = 1.22e0;
gradhi[5] = -1.e0;
break;
case 2:
t = 9.8e4/(x[4]*x[9]+1.e3*x[3]);
t1 = t/(x[4]*x[9]+1.e3*x[3])*x[3];
gradhi[3] = t-1.e3*t1;
gradhi[4] = -x[9]*t1;
gradhi[9] = -x[4]*t1;
gradhi[6] = -1.e0;
break;
case 3:
gradhi[1] = -(x[2]+x[5])/pow(x[1],2);
gradhi[2] = 1.e0/x[1];
gradhi[5] = gradhi[2];
gradhi[8] = -1.e0;
break;
}
return;
}
/* *****************************************************************/
/* compute the i-th inequality constaint, bounds included */
/* *************************************************************** */
void eg(INTEGER i,DOUBLE x[],DOUBLE *gxi) {
static INTEGER k;
static DOUBLE og[11] = {0.,/* not used : index 0 */
2.e3 ,16.e3, 1.2e2,5.e3, 2.e3,
93.e0,95.e0,12.e0, 4.e0,162.e0 };
static DOUBLE ug[11] = {0.,/* not used : index 0 */
1.e-5, 1.e-5,1.e-5,1.e-5, 1.e-5,
85.e0, 90.e0 ,3.e0 ,1.2e0,145.e0 };
static DOUBLE a = .99e0,b = .9e0,c = 2.01010101010101e-2,
d = 2.11111111111111e-1;
static DOUBLE t;
k = (i+1)/2;
switch (k) {
case 1:
t = 35.82e0-.222e0*x[10]-b*x[9];
if(k+k == i) t = -t+x[9]*d;
*gxi = t;
break;
case 2:
t = -133.e0+3.e0*x[7]-a*x[10];
if(k+k == i) t = -t+c*x[10];
*gxi = t;
break;
case 3:
t = 1.12e0*x[1]+.13167e0*x[1]*x[8]-.00667e0*x[1]*pow(x[8],2)-a*x[4];
if(k+k == i) t = -t+c*x[4];
*gxi = t;
break;
case 4:
t = 57.425e0+1.098e0*x[8]-.038e0*pow(x[8],2)+.325e0*x[6]-a*x[7];
if(k+k == i) t = -t+c*x[7];
*gxi = t;
break;
default:
if( i > 18 ) *gxi = og[i-18]-x[i-18];
if( i <= 18 ) *gxi = x[i-8]-ug[i-8];
}
return;
}
/* *************************************************************** */
/* compute the gradient of the i-th inequality constraint */
/* not necessary for bounds, but constant gradients must be set */
/* here e.g. using dcopy from a data-field */
/* *************************************************************** */
void egradg(INTEGER i,DOUBLE x[],DOUBLE gradgi[]) {
static INTEGER j,k;
static DOUBLE a = .99e0,b = .9e0,c = 1.01010101010101e0,
d = 1.11111111111111e0;
for ( j = 1 ; j <= NX ; j++) {
gradgi[j] = 0.e0;
}
k = (i+1)/2;
switch (k) {
case 1:
if ( k+k != i ) {
gradgi[ 9] = -b;
gradgi[10] = -.222e0;
} else {
gradgi[ 9] = d;
gradgi[10] = .222e0;
}
break;
case 2:
if ( k+k != i ) {
gradgi[ 7] = 3.e0;
gradgi[10] = -a;
} else {
gradgi[ 7] = -3.e0;
gradgi[10] = c;
}
break;
case 3:
gradgi[1] = 1.12e0+.13167e0*x[8]-.00667e0*pow(x[8],2);
gradgi[4] = -a;
gradgi[8] = .13167e0*x[1]-.01334e0*x[1]*x[8];
if( k+k == i ) {
gradgi[1] = -gradgi[1];
gradgi[8] = -gradgi[8];
gradgi[4] = c;
}
break;
case 4:
gradgi[6] = .325e0;
gradgi[7] = -a;
gradgi[8] = 1.098e0-.076e0*x[8];
if(k+k == i) {
gradgi[6] = -.325e0;
gradgi[7] = c;
gradgi[8] = -gradgi[8];
}
break;
default:
if( i > 18 ) gradgi[i-18] = -1.e0;
if( i <= 18 ) gradgi[i-8] = 1.e0;
break;
}
return;
}
}
Now the same problem coded in SIF:
***************************
* SET UP THE INITIAL DATA *
***************************
NAME HS114
* Problem :
* *********
* An alkylation process problem.
* Source: problem 114 in
* W. Hock and K. Schittkowski,
* "Test examples for nonlinear programming codes",
* Lectures Notes in Economics and Mathematical Systems 187, Springer
* Verlag, Heidelberg, 1981.
* SIF input: J.M. Collin, Jan 1990.
* classification QOR2-MY-10-11
* Number of variables
IE N 10
* Others Parameters
IE 1 1
RE A 0.99
RE B 0.9
RM -A A -1.0
RM -B B -1.0
RD INVA A 1.0
RD INVB B 1.0
RM -INVA INVA -1.0
RM -INVB INVB -1.0
VARIABLES
DO I 1 N
X X(I)
ND
GROUPS
* Objective Function
N OBJ X2 0.035 X3 10.0
N OBJ X5 3.36 X1 5.04
* Constraint function
G C1 X10 -0.222
ZG C1 X9 -B
G C2 X7 3.0
ZG C2 X10 -A
G C3 X10 0.222
ZG C3 X9 INVB
ZG C4 X10 INVA
G C4 X7 -3.0
G C5 X1 1.12
ZG C5 X4 -A
G C6 X8 1.098 X6 0.325
ZG C6 X7 -A
G C7 X1 -1.12
ZG C7 X4 INVA
G C8 X8 -1.098 X6 -0.325
ZG C8 X7 INVA
E C9 X4 1.22 X1 -1.0
E C9 X5 -1.0
E C10 X6 -1.0
E C11 X8 -1.0
CONSTANTS
HS114 C1 -35.82
HS114 C2 133.0
HS114 C3 35.82
HS114 C4 -133.0
HS114 C6 -57.425
HS114 C8 57.425
BOUNDS
LO HS114 X1 0.00001
UP HS114 X1 2000.0
LO HS114 X2 0.00001
UP HS114 X2 16000.0
LO HS114 X3 0.00001
UP HS114 X3 120.0
LO HS114 X4 0.00001
UP HS114 X4 5000.0
LO HS114 X5 0.00001
UP HS114 X5 2000.0
LO HS114 X6 85.0
UP HS114 X6 93.0
LO HS114 X7 90.0
UP HS114 X7 95.0
LO HS114 X8 3.0
UP HS114 X8 12.0
LO HS114 X9 1.2
UP HS114 X9 4.0
LO HS114 X10 145.0
UP HS114 X10 162.0
START POINT
HS114 X1 1745.0
HS114 X2 12000.0
HS114 X3 110.0
HS114 X4 3048.0
HS114 X5 1974.0
HS114 X6 89.2
HS114 X7 92.8
HS114 X8 8.0
HS114 X9 3.6
HS114 X10 145.0
ELEMENT TYPE
* Element : W * X ** 2
EV WSQ X
EP WSQ W
* Element : W * (X * Y)
EV PROD X Y
EP PROD W
* Element : W * (X * Y ** 2)
EV PROD2 X Y
EP PROD2 W
* Element : (W * X)/(S * T + 1000 * U)
EV RAP1 X S
EV RAP1 T U
EP RAP1 W
* Element : (X + Y)/Z
EV RAP2 X Y
EV RAP2 Z
IV RAP2 SUM SUMZ
ELEMENT USES
T OE1 PROD
V OE1 X X4
V OE1 Y X7
P OE1 W -0.063
T CE1 PROD
V CE1 X X1
V CE1 Y X8
P CE1 W 0.13167
T CE2 PROD2
V CE2 X X1
V CE2 Y X8
P CE2 W -0.00667
T CE3 WSQ
V CE3 X X8
P CE3 W -0.038
T CE4 PROD
V CE4 X X1
V CE4 Y X8
P CE4 W -0.13167
T CE5 PROD2
V CE5 X X1
V CE5 Y X8
P CE5 W 0.00667
T CE6 WSQ
V CE6 X X8
P CE6 W 0.038
T CE7 RAP1
V CE7 X X3
V CE7 S X4
V CE7 T X9
V CE7 U X3
P CE7 W 98000.0
T CE8 RAP2
V CE8 X X2
V CE8 Y X5
V CE8 Z X1
GROUP USES
E OBJ OE1
E C5 CE1 CE2
E C6 CE3
E C7 CE4 CE5
E C8 CE6
E C10 CE7
E C11 CE8
OBJECT BOUND
* Solution
*LO SOLTN -1768.80696
ENDATA
***********************
* SET UP THE FUNCTION *
* AND RANGE ROUTINES *
***********************
ELEMENTS HS114
TEMPORARIES
R WX
R DENOM
INDIVIDUALS
T WSQ
F W * X ** 2
G X 2.0 * W * X
H X X 2.0 * W
T PROD
F W * X * Y
G X W * Y
G Y W * X
H X Y W
T PROD2
F W * X * Y ** 2
G X W * Y ** 2
G Y 2.0 * W * X * Y
H X Y 2.0 * W * Y
H Y Y 2.0 * W * X
T RAP1
A WX W * X
A DENOM S * T + 1000.0 * U
F WX / DENOM
G X W / DENOM
G S - WX * T / DENOM ** 2
G T - WX * S / DENOM ** 2
G U - 1000.0 * WX / DENOM ** 2
H X S - W * T/ DENOM ** 2
H X T - W * S/ DENOM ** 2
H X U - 1000.0 * W / DENOM ** 2
H S S 2.0 * WX * T * T / DENOM ** 3
H S T 2.0 * WX * S * T / DENOM ** 3
H+ - WX / DENOM ** 2
H S U 2000.0 * WX * T / DENOM ** 3
H T T 2.0 * WX * S * S / DENOM ** 3
H T U 2000.0 * WX * S / DENOM ** 3
H U U 2000000.0 * WX / DENOM ** 3
T RAP2
R SUMZ Z 1.0
R SUM X 1.0 Y 1.0
F SUM / SUMZ
G SUM 1.0 / SUMZ
G SUMZ - SUM / SUMZ ** 2
H SUM SUMZ - 1.0 / SUMZ ** 2
H SUMZ SUMZ 2.0 * SUM / SUMZ ** 3
ENDATA