

Next: Conclusion
Up: Numerical examples
Previous: Example 5
In this section we consider an optimal control problem for a semilinear elliptic equation of logistic type which was studied in Leung, Stojanovic
[21,28]. The problem is to determine a distributed control
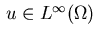 that minimizes the functional
that minimizes the functional
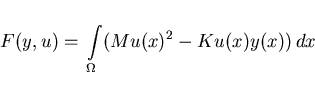 |
(4.7) |
subject to the elliptic state equation
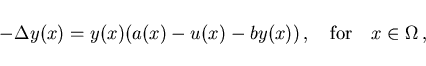 |
(4.8) |
homogeneous Neumann boundary conditions,
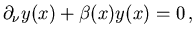 |
|
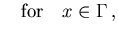 |
(4.9) |
and
control and state inequality constraints
| |
|
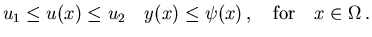 |
(4.10) |
Figure 11:
Example 6 : Optimal control.
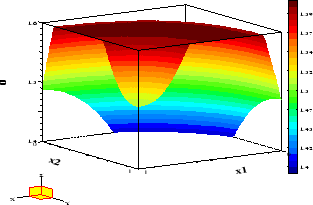 |
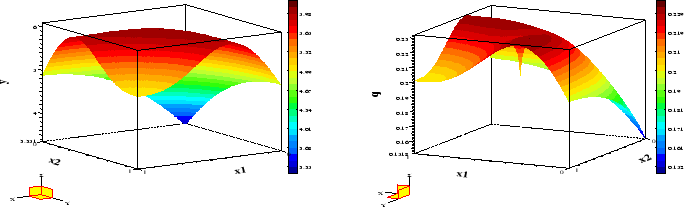
Figure 12:
Example 6 : Optimal state and adjoint variable
 |
Here, 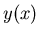 denotes
the population of a biological species,
denotes
the population of a biological species, 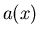 a spatially dependent
intrinsic growth rate,
a spatially dependent
intrinsic growth rate, 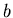 the crowding effect, while
the crowding effect, while 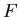 denotes the
difference between economic cost and revenue,
with nonnegative constants
denotes the
difference between economic cost and revenue,
with nonnegative constants 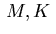 .
In [21,28] the function
.
In [21,28] the function 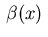 was chosen as
was chosen as 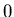 .
Numerical results for this case can be found in [25].
Here, we consider
.
Numerical results for this case can be found in [25].
Here, we consider
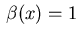 if
if
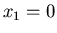 or
or 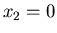 and
and
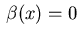 otherwise.
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [8].
otherwise.
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [8].
The adjoint equations (2.10), (2.11) yield the following
equations:
For 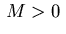 , the minimum condition (2.18) gives
the control law
, the minimum condition (2.18) gives
the control law
![\begin{displaymath}
\bar{u}(x) = P_{\,[u_1,u_2]}
\left ( \frac{1}{2M}\,[\,(K - \bar{q}(x))\,\bar{y}(x)\,] \right ) \,,
\end{displaymath}](img210.gif) |
(4.11) |
where
![$\,P_{\,[u_1,u_2]}\,$](img147.gif) denotes the projection operator on the interval
denotes the projection operator on the interval
![$\,[u_1,u_2]\,$](img211.gif) .
.
The following concrete data were used:
Figure 11 displays the optimal control while Figure 12 shows
the optimal state and adjoint variable.
The reader may verify that the minimum condition given
by the projection (4.11) holds with high accuracy.
However, note that condition (2.7) imposed in [6]
is not satisfied everywhere in 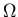 .
.
Table 7:
Information on solution of Example 6
| N+1 |
it |
CPU |
Acc |
 |
| 50 |
29 |
104 |
8 |
-4.19322 |
| 100 |
32 |
2235 |
8 |
-4.27569 |
| 200 |
33 |
42543 |
8 |
-4.31709 |
|


Next: Conclusion
Up: Numerical examples
Previous: Example 5
Hans D. Mittelmann
2000-10-06
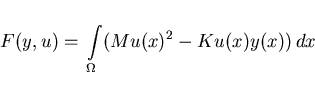
![]() denotes
the population of a biological species,
denotes
the population of a biological species, ![]() a spatially dependent
intrinsic growth rate,
a spatially dependent
intrinsic growth rate, ![]() the crowding effect, while
the crowding effect, while ![]() denotes the
difference between economic cost and revenue,
with nonnegative constants
denotes the
difference between economic cost and revenue,
with nonnegative constants ![]() .
In [21,28] the function
.
In [21,28] the function ![]() was chosen as
was chosen as ![]() .
Numerical results for this case can be found in [25].
Here, we consider
.
Numerical results for this case can be found in [25].
Here, we consider
![]() if
if
![]() or
or ![]() and
and
![]() otherwise.
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [8].
otherwise.
The goal is to
find a control function which maximizes profit.
A similar control problem with Dirichlet boundary conditions was recently
studied by Cañada et al. [8].
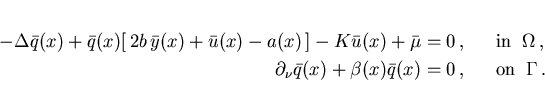
![\begin{displaymath}
\begin{array}{l}
a(x) = 7 + 4 \sin(2\pi x_1 x_2),\,b = 1,\,M...
...=0.8,
\\ [1mm]
u_1=1.4,\,u_2=1.6, \,\psi(x)=6.09\,.
\end{array}\end{displaymath}](img212.gif)