

Next: Steady Progressing Wave Solutions
Up: No Title
Previous: No Title
Transitions from rest to oscillatory behavior
can occur in mathematical models of neural
networks in a variety of ways.
One way is through
the disappearance of an impediment to oscillation,
such as
coalescence and disappearance of stable and unstable
rest states lying on a stable limit cycle,
resulting in a stable oscillation.
This phenomenon is
referred to as being a saddle-node bifurcation on a limit cycle (SNLC)
[9]. The SNLC and the Hopf bifurcation are the simplest
ones exhibiting the onset of oscillations in the sense that
they have codimension one; i.e., they have the fewest
restrictions.
SNLC bifurcations are observed in the neurobiological models
[1], and
a canonical model for a SNLC bifurcation
is the VCON model developed in
[2, 3]. (VCON denotes voltage controlled oscillator
neuron model.) The integrate-and-fire model [14]
also exhibits this type of bifurcation, and in this sense
it is closely related to the VCON.
We describe here some interesting aspects of wave propagation in
networks that are near multiple SNLCs by studying networks of VCONs.
This work is related to modeling regions of the neocortex
and other brain structures [5,7], and
these models are similar
to many others that have been derived for parts of the neocortex
using neurooscillators [8,15].
An advantage of the VCON model is that it enables one to study
information flow in networks using routine frequency domain methods.
A VCON network is described by the model [2,3]
where
-
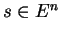 for
for
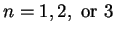 addresses sites.
addresses sites.
-
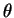 is a vector of phase variables taking values
in EN.
is a vector of phase variables taking values
in EN.
-
-
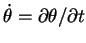 .
.
-
- The connection matrix kernel
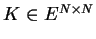 is L periodic in each dimension of s.
We suppose here that
K describes isotropic connections: K=K(s-s').
It describes the amplitude of connections from s' to s.
is L periodic in each dimension of s.
We suppose here that
K describes isotropic connections: K=K(s-s').
It describes the amplitude of connections from s' to s.
-
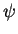 describes the polarity of connections from s' to s.
It is also L-periodic.
describes the polarity of connections from s' to s.
It is also L-periodic.
-
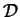 is a domain in the space of interest. In our case, we
consider this set to be
is a domain in the space of interest. In our case, we
consider this set to be
![${\cal D}=[-L,L]^n$](img14.gif) for
for
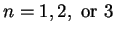 .
.
-
- The vector of functions
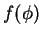 is
is 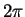 -periodic
in each component of
-periodic
in each component of
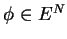 .
.
-
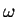 is the vector of center frequencies of the network
elements.
is the vector of center frequencies of the network
elements.
This model can be derived from
general networks that are operating
near a multiple SNLC bifurcation [7].
It has a rich structure of wavelike solutions,
and it will be studied in
greater detail elsewhere. We wish here to identify
steady progressing wave
solutions of this system, describe their stability properties,
and illustrate them
through computer simulations.


Next: Steady Progressing Wave Solutions
Up: No Title
Previous: No Title
Hans Mittelmann
2000-04-04