

Next: MOSEK
Up: The Codes
Previous: DSDP
Authors: Toh, Todd, Tütüncü
Version: 3.0, 7/2001;
Available: yes, from http://www.math.nus.edu.sg/ mattohkc/sdpt3.html
Key paper: [26]
Features: primal-dual method, infeasible primal-dual and homogeneous self-dual formulations, Lanczos steplength computation
Language, Input format: Matlab+C or Fortran; SDPA
Error computations: yes
Solves: SDP and SOCP
This code is designed to solve conic programming problems whose constraint
cone is a product of semidefinite cones, second-order cones, and/or
nonnegative orthants. It employs a predictor-corrector
primal-dual path-following method, with
either the H..K..M or the NT search direction. The basic code is written
in Matlab, but key subroutines in Fortran and C are incorporated via
Mex files. Routines are provided to read in problems in either SeDuMi
or SDPA format. Sparsity and block diagonal structure are exploited,
but the latter needs to be given explicitly.
The algorithm is stopped if:
Remarks:
- SDPT3 is a general-purpose code based on a polynomial-time interior-point
method.
- It should obtain reasonably accurate solutions to problems of
small and medium size (for problems with semidefinite constraints, up to
around a thousand constraints involving matrices of order up to around
a thousand, and for sparse problems with only second-order/linear cones, up to
around 20,000 constraints and 50,000 variables), and can solve some larger
problems.
- Because it uses a primal-dual strategy, forms the Schur complement
matrix for the Newton equations, and employs direct methods, it is unlikely
to compete favorably with alternative methods on large-scale problems.


Next: MOSEK
Up: The Codes
Previous: DSDP
Hans D. Mittelmann
2002-08-17
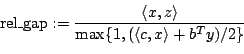
![\begin{displaymath}
\mbox{infeas\_meas} := \max \left[
\frac{\Vert\mathcal{A}x ...
...t\mathcal{A}^* y + z - c\Vert}{\max\{1,\Vert c\Vert\}} \right]
\end{displaymath}](img98.gif)
![]()
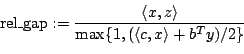
![\begin{displaymath}
\mbox{infeas\_meas} := \max \left[
\frac{\Vert\mathcal{A}x ...
...t\mathcal{A}^* y + z - c\Vert}{\max\{1,\Vert c\Vert\}} \right]
\end{displaymath}](img98.gif)
![]()